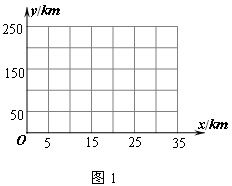
一次函数y=k x+b的图像经过点(0,-4)且与正比例函数y=k
x+b的图像经过点(0,-4)且与正比例函数y=k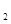 x的图象交于点(2,-1).
x的图象交于点(2,-1).
(1)分别求出这两个函数的表达式;
(2)求这两个函数的图象与x轴围成的三角形的面积;
(3)直接写出不等式k x-4≥k
x-4≥k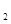 x的解集。
x的解集。
.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
某商场将进货价为30元的台灯以40元售出,平均每月能售出600个,调查发现,售价在40元至60元范围内,台灯的售价每上涨1元,其销售量就将减少10个。为了实现平均每月10000元的销售利润,这种台灯应涨价多少元?这时应购进台灯多少个?
已知:如图1,△OAB是边长为2的等边三角形,OA在x轴上,点B在第一象限内;△OCA是一个等腰三角形,OC=AC,顶点C在第四象限,∠C=120°.现有两动点P、Q分别从A、O两点同时出发,点Q以每秒1个单位的速度沿OC向点C运动,点P以每秒3个单位的速度沿A→O→B运动,当其中一个点到达终点时,另一个点也随即停止.
(1)求在运动过程中形成的△OPQ面积S与运动时间t之间的函数关系,并写出自变量t的取值范围;
(2)在OA上(点O、A除外)存在点D,使得△OCD为等腰三角形,请直接写出所有符合条件的点D的坐标;
(3)如图2,现有∠MCN=60°,其两边分别与OB、AB交于点M、N,连接MN.将∠MCN绕着C点旋转(0°<旋转角<60°),使得M、N始终在边OB和边AB上.试判断在这一过程中,△BMN的周长是否发生变化?若没有变化,请求出其周长;若发生变化,请说明理由.
8分,如图,在平面直角坐标系 中,已知直线
中,已知直线 的解析式为
的解析式为 ,直线
,直线 交
交 轴于点
轴于点 ,交
,交 轴于点
轴于点 .
.
(1)若一个等腰直角三角形OBD的顶点D与点C重合,直角顶点B在第一象限内,请直接写出点B的坐标;
(2)过点B作x轴的垂线l,在l上是否存在一点P,使得△AOP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)试在直线AC上求出到两坐标轴距离相等的所有点的坐标.
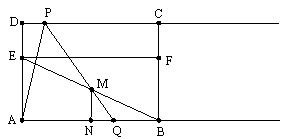
如图,在矩形ABCD中,AB=6,AD= ,点E是AD的三等分点,且AE
,点E是AD的三等分点,且AE DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为
DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为 .
.
(1)当点Q与点B重合时,求DP的长度;
(2)设AB的中点为N,PQ与线段BE相交于点M,是否存在点P,使△ 为等腰三角形?若存在,请直接写出时间
为等腰三角形?若存在,请直接写出时间 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)设△ 与四边形
与四边形 的重叠部分的面积为S,试求S与
的重叠部分的面积为S,试求S与 的函数关系式和相应的自变量
的函数关系式和相应的自变量 的取值范围.
的取值范围.
(本小题满分8分)如图所示,反比例函数y1的图象经过点A(3,2),解答下列问题: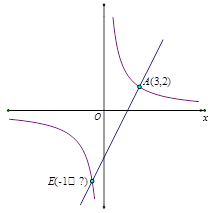
(1)求y1的函数关系式;
(2)过y1上任意一点B向x轴,y轴作垂线,交两坐标轴于C,D两点,求矩形OCBD的面积;
(3)过点A的一次函数y2与反比例函数y1的另一个交点E的横坐标为-1,求y2的关系式;
(4)通过图象回答当x取何值时,y1>y2;
如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.
(1)赛道的长度是 m,甲的速度是 m/s;
(2)经过多少秒时,甲、乙两人第二次相遇?
(3)若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了 次.2分钟时,乙距池边B1B2的距离为多少米.
已知一次函数y=2x-k与反比例函数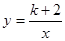 的图像相交于A和B两点.,如果有一个交点A的横坐标为3,
的图像相交于A和B两点.,如果有一个交点A的横坐标为3,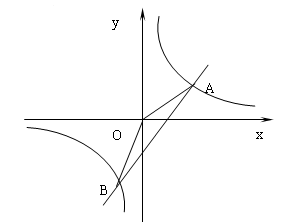
(1)求k的值;
(2)求A、B两点的坐标;
(3)根据图象写出一次函数的值大于反比例函数的值的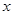 的取值范围
的取值范围
(4)求△AOB的面积;
如图,已知反比例函数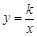 的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线 y="ax+b" 经过点A,并且经过反比例函数
的图像经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB 的面积为2.若直线 y="ax+b" 经过点A,并且经过反比例函数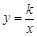 的图象上另一点C(n,一2).
的图象上另一点C(n,一2).
(1)求反比例函数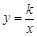 与直线y=ax+b的解析式;
与直线y=ax+b的解析式;
(2)根据所给条件,直接写出不等式 ax+b≥ 的解集_________________;
的解集_________________;
(3)求出线段OA的长,并思考:在x轴上是否存在一点P,使得△PAO是等腰三角形,如果存在,请求出P的坐标,如果不存在,请说明理由。
为了预防H7N9禽流感,某学校对教室采用药熏消毒法进行消毒.已知,药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧后,y与x成反比例(如图所示).现测得药物4分钟燃毕,此室内空气中每立方米的含药量为8毫克,请你根据题中所提供的信息,解答下列问题:
(1)求出药物燃烧时与药物燃烧后y与x的函数关系式,并写出相应的自变量的取值范围 。
(2)研究表明,当空气中每立方米的含药量不低于2毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?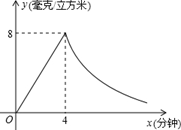
在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.
(1)求点C的坐标;
(2)若∠ACB的平分线所在的直线l交x轴于点D,求直线l对应的一次函数关系式;
(3)过点D任作一直线l′分别交射线CA、CB(点C除外)于点M、N,则 +
+ 的值是否为定值?若是,求出定值;若不是,请说明理由.
的值是否为定值?若是,求出定值;若不是,请说明理由.
如图,二次函数的图象与x轴交与A(4,0),并且OA=OC=4OB,点P为过A、B、C三点的抛物线上一动点.
(1)求点B、点C的坐标并求此抛物线的解析式;
(2)是否存在点P,使得△ACP是以点C为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
如图,已知A(-4,2)、B(n,-4)是一次函数y=kx+b的图象与反比例函数y= 的图象的两个交点.
的图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
如图1,A,B,C为三个超市.在A通往C的道路(粗实线部分)上有一D点,D与B有道路(细实线部分)相通这.A与D,D与C,D与B之间的路程分别为25㎞,10㎞,5㎞.现计划在A通往C的道路上建一个配货中心H,每天有一辆货车只为这三个超市送货.该货车每于从H出发,单独为A送货1次,为B送货1次,为C送货2次.货车每次仅能给一家超市送货,每次送货后均返回配货中心H.设H到A的路程为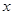 ㎞,这辆货车每天行驶的路程为
㎞,这辆货车每天行驶的路程为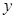 ㎞.
㎞.

(1)用含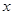 的代数式填空:当0≤
的代数式填空:当0≤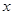 ≤25时货车从H到A往返1次的路程为2
≤25时货车从H到A往返1次的路程为2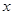 ㎞,货车从H到B往返1次的路程为 ㎞;货车从H到C往返2次的路程为 ㎞;这辆货车每天行驶的路程
㎞,货车从H到B往返1次的路程为 ㎞;货车从H到C往返2次的路程为 ㎞;这辆货车每天行驶的路程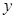 = ;当25<
= ;当25<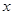 ≤35时,这辆货车每天行驶的路程
≤35时,这辆货车每天行驶的路程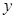 = ;
= ;
(2)请在图2中画出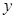 与
与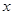 (0≤
(0≤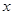 ≤35)的函数图象;
≤35)的函数图象;
(3)配货中心H建在哪段,这辆货车每天行驶的路程最短?