初中数学一次函数的最值解答题

如图，已知一次函数的图象与x轴交于点A，与二次函数的图象交于y轴上的一点B，二次函数的图象与x轴只有唯一的交点C，且OC=2．

（1）求二次函数的解析式；
（2）设一次函数的图象与二次函数的图象的另一交点为D，已知P为x轴上的一个动点，且△PBD为直角三角形，求点P的坐标．

某车间的甲、乙两名工人分别同时生产只同一型号的零件，他们生产的零件（只）与生产时间的函数关系的图象如图所示。根据图象提供的信息解答下列问题：

（1）甲每分钟生产零件_______只；乙在提高生产速度之前已生产了零件_______只；
（2）若乙提高速度后，乙的生产速度是甲的倍，请分别求出甲、乙两人生产全过程中，生产的零件（只）与生产时间的函数关系式；
（3）当两人生产零件的只数相等时，求生产的时间；并求出此时甲工人还有多少只零件没有生产．

如图所示，已知一次函数（k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数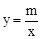（m≠0）的图象在第一象限交于C点，CD垂直于x轴，垂足为D．若OA=OB=OD=1．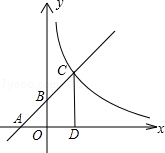

（1）求点A、B、D的坐标；
（2）求一次函数和反比例函数的解析式．

如图，抛物线与x轴交于点A（2，0），交y轴于点B（0，）．直线过点A与y轴交于点C，与抛物线的另一个交点是D．

（1）求抛物线与直线的解析式；
（2）设点P是直线AD上方的抛物线上一动点（不与点A、D重合），过点P作 y轴的平行线，交直线AD于点M，作DE⊥y轴于点E．探究：是否存在这样的点P，使四边形PMEC是平行四边形？若存在请求出点P的坐标；若不存在，请说明理由；
（3）在（2）的条件下，作PN⊥AD于点N，设△PMN的周长为l，点P的横坐标为x，求l与x的函数关系式，并求出l的最大值．

四川省第十二届运动会将于2014年8月18日在我市隆重开幕，根据大会组委会安排，某校接受了开幕式大型团体操表演任务．为此，学校需要采购一批演出服装，A、B两家制衣公司都愿成为这批服装的供应商．经了解：两家公司生产的这款演出服装的质量和单价都相同，即男装每套120元，女装每套100元．经洽谈协商：A公司给出的优惠条件是，全部服装按单价打七折，但校方需承担2200元的运费；B公司的优惠条件是男女装均按每套100元打八折，公司承担运费．另外根据大会组委会要求，参加演出的女生人数应是男生人数的2倍少100人，如果设参加演出的男生有x人．
（1）分别写出学校购买A、B两公司服装所付的总费用y₁（元）和y₂（元）与参演男生人数x之间的函数关系式；
（2）问：该学校购买哪家制衣公司的服装比较合算？请说明理由．

如图，抛物线关于直线对称，与坐标轴交于A、B、C三点，且AB=4，点D在抛物线上，直线是一次函数的图象，点O是坐标原点.

（1）求抛物线的解析式；
（2）若直线平分四边形OBDC的面积，求k的值.
（3）把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线与直线交于M、N两点，问在y轴正半轴上是否存在一定点P，使得不论k取何值，直线PM与PN总是关于y轴对称？若存在，求出P点坐标；若不存在，请说明理由.

如图，在平面直角坐标系中，直线y=－x－3与抛物线y=x²＋mx＋n相交于两个不同的点A、B，其中点A在x轴上．

（1）则A点坐标为   ；
（2）若点B为该抛物线的顶点，求m、n的值；
（3）在（2）条件下，设该抛物线与x轴的另一个交点为C，请你探索在平面内是否存在点D，使得△DAC与△DCO相似？如果存在，求出点D的坐标；如果不存在，请说明理由．

某公司生产一种环保产品，需要添加一种新型原料，若每件产品的利润与新型原料价格成一次函数关系，且每件产品的利润y（元）与新型原料的价格x（元/千克）的函数图象如图：

（1）当新型原料的价格为600元/千克时，每件产品的利润是多少？
（2）新型原料是一种稀少材料，为了珍惜资源，政府部门规定：新型原料每天使用量m（千克）与价格x（元/千克）的函数关系为x ="10m" +500，且m千克新型原料可生产10m件产品．那么生产300件这种产品，一共可得利润是多少？
（3）受生产能力的限制，该公司每天生产这种产品不超过450件，那么在（2）的条件下，该公司每天应生产多少件产品才能获得最大利润？最大利润是多少？

在数学学习中，及时对知识进行归纳和整理是改善学习的重要方法．善于学习的小明在学习了一次方程（组）、一元一次不等式和一次函数后，把相关知识归纳整理如下：

（1）请你根据以上方框中的内容在下面数字序号后写出相应的结论：
①          ；②          ；③          ；④          ；
（2）如果点的坐标为（1，3），那么不等式的解集是          ．

（本小题满分8分）某技工培训中心有钳工20名、车工30名. 现将这50名技工中的15人派往A地工作，35人派往B地工作，两地技工的工资情况如下表：

工种 属地	钳工	车工
地	1800（元/月）	1600（元/月）
地	1600（元/月）	1200（元/月）

 
设派往A地x名钳工时，这50名技工的月工资总额为y元.
（1）派往B地___________名钳工，派往B地___________名车工；
（2）求y关于x的函数关系式；
（3）若A地钳工的月工资总额不小于B地钳工的月工资总额，派往A地多少名钳工，可使这50名技工的月工资总额最高？

某玉米种子的价格为a元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打8折，某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析，并绘制出了函数图象，以下是该科技人员绘制的图象和表格的不完全资料，已知点A的坐标为（2，10），请你结合表格和图象：

付款金额（元）	a	7．5	10	12	b
购买量（千克）	1	1．5	2	2．5	3

 
（1）指出付款金额和购买量哪个变量是函数的自变量x，并写出表中a、b的值；
（2）求出当x＞2时，y关于x的函数解析式；
（3）甲农户将88元钱全部用了购买该玉米种子，乙农户购买了4165克该玉米种子，分别计算他们的购买量和付款金额．

（本小题满分11分）如图，在平面直角坐标系中，矩形ABCD的顶点A、B、C的坐标分别为（0，5）（0，2）（4，2），直线l的解析式为y = kx+5－4k（k > 0）．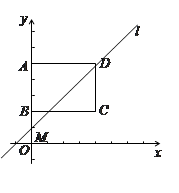

（1）当直线l经过点B时，求一次函数的解析式；
（2）通过计算说明：不论k为何值，直线l总经过点D；
（3）直线l与y轴交于点M，点N是线段DM上的一点， 且△NBD为等腰三角形，试探究：
①当函数y = kx+5－4k为正比例函数时，点N的个数有      个；
②点M在不同位置时，k的取值会相应变化，点N的个数情况可能会改变，请直接写出点N所有不同的个数情况以及相应的k的取值范围．

某学校开展“青少年科技创新比赛”活动，“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型．甲、乙两车同时分别从A，B两处出发，沿轨道到达C处，B在AC上，甲的速度是乙的速度的1．5倍，设t后甲、乙两遥控车与B处的距离分别为d₁，d₂，则d₁，d₂与t的函数关系如图，试根据图象解决下列问题：

（1）填空：乙的速度v₂=        米/分；
（2）写出d₁与t的函数关系式：
（3）若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰，试探求什么时间两遥控车的信号不会产生相互干扰？

一次函数y=kx+b的图像经过点（0，-4）且与正比例函数y=k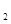x的图象交于点（2，-1）．
（1）分别求出这两个函数的表达式；
（2）求这两个函数的图象与x轴围成的三角形的面积；       
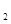（3）直接写出不等式kx-4≥kx的解集。

．某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．
（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式；
（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本＝每件的成本×每天的销售量）