初中数学一次函数的最值解答题

为了解都匀市交通拥堵情况，经统计分析，都匀彩虹桥上的车流速度v（千米/时）是车流密度x（辆/千米）的函数，当桥上的车流密度达到220辆/千米时，造成堵塞，此时车流速度为0千米/时；当车流密度为20辆/千米时，车流速度为80千米/时．研究表明：当20≤x≤220时，车流速度v是车流密度x的一次函数．
（1）求彩虹桥上车流密度为100辆/千米时的车流速度；
（2）在交通高峰时段，为使彩虹桥上车流速度大于40千米/时且小于60千米/时，应控制彩虹桥上的车流密度在什么范围内？
（3）当车流量（辆/小时）是单位时间内通过桥上某观测点的车辆数，即：车流量=车流速度×车流密度．当20≤x≤220时，求彩虹桥上车流量y的最大值．

如图，在平面直角坐标系中，O为坐标原点．A．B两点的坐标分别为A（m，0）、B（0，n），且，点P从A出发，以每秒1个单位的速度沿射线AO匀速运动，设点P运动时间为t秒．
（1）求m、n的值与OA、OB的长；
（2）连接PB，若△POB的面积不大于3且不等于0，则t的取值范围是          （请直接写出答案）．
（3）过P作直线AB的垂线，垂足为D，直线PD与y轴交于点E，在点P运动的过程中，是否存在这样的点P，使△EOP≌△AOB？若存在，请求出t的值；若不存在，请说明理由．
        

如图，直线y=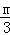x+m（m≠0）交x轴负半轴于点A、交y轴正半轴于点B且AB=5，过点A作直线AC⊥AB交y轴于点C．点E从坐标原点O出发，以0.8个单位/秒的速度沿y轴向上运动；与此同时直线l从与直线AC重合的位置出发，以1个单位/秒的速度沿射线AB方向平行移动．直线l在平移过程中交射线AB于点F、交y轴于点G．设点E离开坐标原点O的时间为t（t≥0）s．
（1）求直线AC的解析式；
（2）直线l在平移过程中，请直接写出△BOF为等腰三角形时点F的坐标；
（3）直线l在平移过程中，设点E到直线l的距离为d，求d与t的函数关系．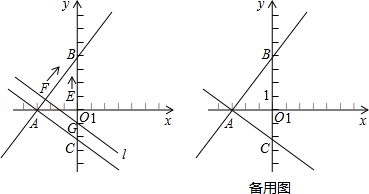

如图，直线y=x+2与x轴交于点A，与y轴交于点B，动点P从点A开始沿折线AB﹣BO以1cm/s的速度运动到点O．设点P运动的时间为t（s），△PAO面积为S（cm²）．（坐标轴的单位长度为cm）

（1）当点P在线段AB上运动到与点O距离最小时，求S的值；
（2）在整个运动过程中，求S与t之间的函数表达式；
（3）当点P运动几秒后，△PAO面积为2cm²？

正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形。

（1）如图1中，点A、B、C均在格点上。求出△ABC的面积；
（2）在图2正方形网格（每个小正方形边长为1）中以D为坐标原点建立如图所示的直角坐标系，若格点△DEF满足DE=DF=5，EF=，点E在坐标轴上，请画出符合题意的图形；（注意两解哦！）
（3）求出（2）中直线EF的一次函数表达式。

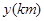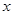一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为，两车之间的距离为，图中的折线表示与之间的函数关系．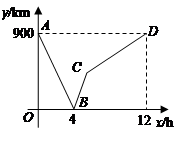

根据图象进行以下探究：
（1）请解释图中点B的实际意义；
（2）求慢车和快车的速度；
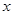（3）求线段BC所表示的与之间的函数关系式，并写出自变量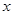的取值范围；

为了能有效地使用电力资源，跃进花园小区实行居民峰谷用电，居民家庭在峰时段（上午8：00—晚上21：00）用电的电价为0．55元/度，谷时段（晚上21：00—次日晨8：00）用电的电价为0．35元/度．
（1）若朱老师家某月用电100度，其中峰时段用电度，这个月应缴纳电费      度；当朱老师家峰时段用电60度时，求应缴纳电费．
（2）朱老师生活节俭，每天早晨5：30起身后立即用额定功率1500瓦的电水壶烧水，10分钟能烧开一壶水。问朱老师家一年内用电水壶烧水共耗电多少度？能节省电费多少元？（一年按实际烧水360天计算，1度=1千瓦．时）

(7分)如图,一次函数y=－x+3的图象与x轴和y轴分别交于点A和B ,再将△AOB沿直线CD对折,使点A与点B重合.直线CD与x轴交于点C,与AB交于点D.

(1)点A的坐标为           ，点B的坐标为            。
(2)求OC的长度;
(3)在x轴上有一点P,且△PAB是等腰三角形,不需计算过程,直接写出点P的坐标.

如图，A（0，1），M（3，2），N（4，4） , 动点P从点A出发，沿y
轴以每秒1个单位长的速度向上移动，且过点P的直线l：y＝－x+b也随之移动，设移动时间为 t 秒.（直线y = kx+b平移时k不变）

（1）当t＝3时，求 l 的解析式；
（2）若点M，N位于l 的异侧，确定 t 的取值范围.

某地出租车计费方法如图所示，x（km）表示行驶里程，y（元）表示车费，请根据图像解答下列问题：

（1）该地出租车的起步价是多少元？
（2）当x＞2时，求y与x之间的函数关系式；
（3）若某乘客有一次乘出租车的里程为18km，则这位乘客需付出租车车费多少元？

如图甲，在平面直角坐标系中，直线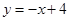分别交x轴、y轴点A、B，⊙O的半径为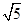个单位长度．点P为直线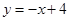上的动点，过点P作⊙O的切线PC、PD ，切点分别为C、D，且PC⊥PD.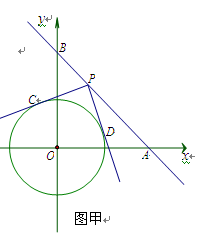

（1）写出点A、B的坐标：A (         )，B (          )；
（2）试说明四边形OCPD的形状（要有证明过程）；
（3）求点P的坐标；
（4）如图乙 ，若直线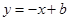将⊙O的圆周分成两段弧长之比为1∶3，请直接写出b的值：b=   ．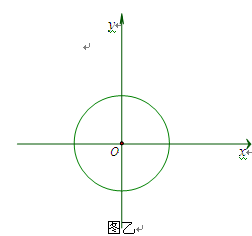

如图，已知一次函数的图象与轴和轴分别相交于A、B两点，点C在线段BA上以每秒1个单位长度的速度从点B向点A运动，同时点D在线段AO上以同样的速度从点A向点O运动，运动时间为，其中一点到达终点时，另一点也随之停止运动.

（1）求线段AB的长；
（2）当为何值时，ACD的面积等于AOB面积的；
（3）当为何值时，ACD是等腰三角形.

如图，已知A（-4，2）、B（n，-4）是一次函数y=kx+b的图象与反比例函数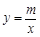 的图象的两个交点．

（1）求此反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值小于反比例函数的值的x的取值范围．

如图，直线：与轴交于点（4，0），与轴交于点，长方形的边在轴上，，．长方形由点与点重合的位置开始，以每秒1个单位长度的速度沿轴正方向作匀速直线运动，当点与点重合时停止运动.设长方形运动的时间为秒，长方形与△重合部分的面积为.

（1）求直线的解析式；
（2）当=1时，请判断点是否在直线上，并说明理由；
（3）请求出当为何值时，点在直线上；
（4）直接写出在整个运动过程中与的函数关系式.

学校需要到印刷厂印刷x份材料，甲印刷厂提出：每份材料收0.2元印刷费，另收500元制版费；乙印刷厂提出：每份材料收0.4元印刷费，不收制版费．
（1）两印刷厂的收费各是多少元？（用含x的代数式表示）
（2）学校要印刷2400份材料，若不考虑其他因素，选择哪家印刷厂比较合算？试说明理由．