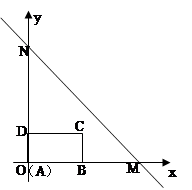
如图,直线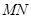 :
: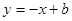 与
与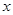 轴交于点
轴交于点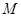 (4,0),与
(4,0),与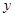 轴交于点
轴交于点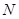 ,长方形
,长方形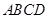 的边
的边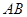 在
在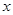 轴上,
轴上,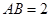 ,
,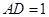 .长方形
.长方形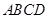 由点
由点 与点
与点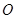 重合的位置开始,以每秒1个单位长度的速度沿
重合的位置开始,以每秒1个单位长度的速度沿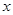 轴正方向作匀速直线运动,当点
轴正方向作匀速直线运动,当点 与点
与点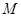 重合时停止运动.设长方形运动的时间为
重合时停止运动.设长方形运动的时间为 秒,长方形
秒,长方形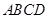 与△
与△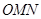 重合部分的面积为
重合部分的面积为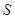 .
.
(1)求直线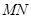 的解析式;
的解析式;
(2)当 =1时,请判断点
=1时,请判断点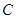 是否在直线
是否在直线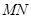 上,并说明理由;
上,并说明理由;
(3)请求出当 为何值时,点
为何值时,点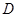 在直线
在直线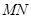 上;
上;
(4)直接写出在整个运动过程中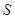 与
与 的函数关系式.
的函数关系式.
相关知识点
推荐套卷
 、
、 、
、 之间的等量关系式.
之间的等量关系式. ,
, ,求
,求 的值.
的值. .
. .
.
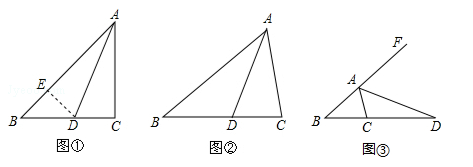
 这样的完全平方式,可以用公式将它分解成
这样的完全平方式,可以用公式将它分解成 的形式,但是,对于二次三项式
的形式,但是,对于二次三项式 就不能直接用完全平方公式,可以采用如下方法:
就不能直接用完全平方公式,可以采用如下方法: =
= =
= .
. 分解因式.
分解因式.






 粤公网安备 44130202000953号
粤公网安备 44130202000953号