河北省邯郸市九年级第一次模拟考试数学试卷
一个等腰三角形的两边长分别是3和7,则它的周长为( )
| A.17 | B.15 | C.13 | D.13或17 |
据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为( )
A.0.3×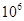 |
B.3×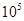 |
C.3×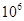 |
D.30× |
如图,AB∥CD,EF⊥AB于点E,EF交CD于点F,已知∠1=60°,则∠2的度数为( )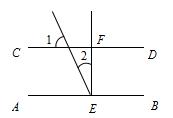
| A.20° | B.60° | C.30° | D.45° |
下图是甲、乙、丙三人玩跷跷板的示意图(支点在中点处),则甲的体重的取值范围在数轴上表示正确的是( )

某篮球队12名队员的年龄如下表所示:
| 年龄(岁) |
18 |
19 |
20 |
21 |
| 人数 |
5 |
4 |
1 |
2 |
则这12名队员年龄的众数和中位数分别是( )
A.18,19 B.18,19.5 C.5,4 D.5, 4.5
二次函数 的大致图象如图所示,关于该二次函数,下列说法错误的是( )
的大致图象如图所示,关于该二次函数,下列说法错误的是( )
| A.函数有最小值 |
B.对称轴是直线x= |
C.当x< 时,y随x的增大而减小 时,y随x的增大而减小 |
| D.当 -1<x<2时,y>0 |
如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于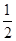 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=250,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=250,则∠ACB的度数为( )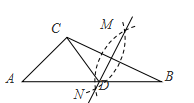
A.90° B. 95° C. 100° D. 105°
如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )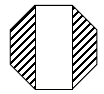
A.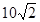 |
B.20 | C.18 | D.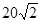 |
如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=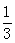 CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为
CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为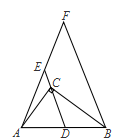
| A.6 | B.7 | C.8 | D.10 |
已知点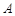 为某封闭图形边界上一定点,动点
为某封闭图形边界上一定点,动点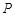 从点
从点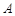 出发,沿其边界顺时针匀速运动一周.设点
出发,沿其边界顺时针匀速运动一周.设点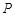 运动的时间为
运动的时间为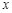 ,线段
,线段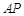 的长为
的长为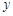 .表示
.表示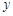 与
与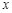 的函数关系的图象大致如右图所示,则该封闭图形可能是( )
的函数关系的图象大致如右图所示,则该封闭图形可能是( )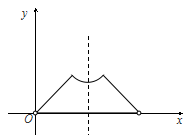
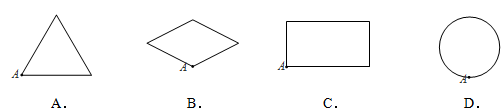
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数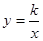 的图象上.若点A的坐标为(-2,-2),则k的值为________.
的图象上.若点A的坐标为(-2,-2),则k的值为________.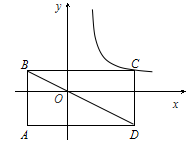
如图10,所有正三角形的一边都与x轴平行,一顶点在y轴正半轴上,顶点依次用A1,A2,
A3,A4…表示,坐标原点O到边A1A2,A4 A5,A7A8…的距离依次是1,2,3,…, 从内到外,正三角形的边长依次为2,4,6,…,则A23的坐标是 .
(本小题满分10分)已知代数式:A= ,B=
,B= .
.
(1)试证明:若A、B均有意义,则它们的值互为相反数;
(2)若代数式A、B中的x是满足不等式3(x-3)<6-2x的正整数解,求A-B的值.
(本小题满分10分)某校为了调查学生书写汉字的能力,从八年级800名学生中随机抽选了50名学生参加测试,这50名学生同时听写50个常用汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出不完整的频数分布表和频数分布直方图如图表: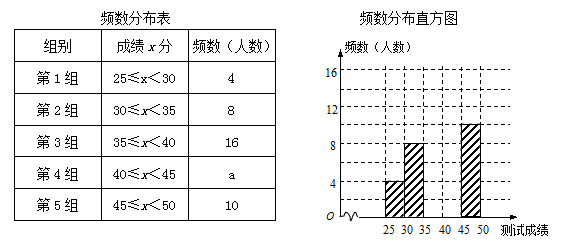
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,请你估计该校八年级汉字书写优秀的人数?
(4)第一组中的A、B、C、D 四名同学为提高汉字书写能力,分成两组,每组两人进行对抗练习,请用列表法或画树状图的方法,求A与B名同学能分在同一组的概率.
(本小题满分11分)在图1——图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM=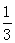 AD,点N是折线AB-BC上的一个动点.
AD,点N是折线AB-BC上的一个动点.
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为________.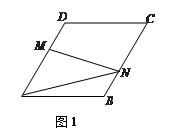
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′ 落在AB边上,则线段AN的长度为________;
②当点A′ 落在对角线AC上时,如图11-3,求证:四边形AM A′N是菱形;
③当点A′ 落在对角线BD上时,如图11-4,求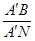 的值.
的值.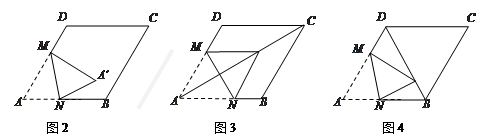
(本小题满分11分)如图,在平面直角坐标系中,矩形ABCD的顶点A、B、C的坐标分别为(0,5)(0,2)(4,2),直线l的解析式为y = kx+5-4k(k > 0).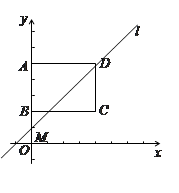
(1)当直线l经过点B时,求一次函数的解析式;
(2)通过计算说明:不论k为何值,直线l总经过点D;
(3)直线l与y轴交于点M,点N是线段DM上的一点, 且△NBD为等腰三角形,试探究:
①当函数y = kx+5-4k为正比例函数时,点N的个数有 个;
②点M在不同位置时,k的取值会相应变化,点N的个数情况可能会改变,请直接写出点N所有不同的个数情况以及相应的k的取值范围.
(本小题满分11分)如图1,在△ABC中,∠ACB=90°,AC=BC=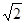 ,以点B为圆心,以1为半径作圆. 设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA,PD,PB,
,以点B为圆心,以1为半径作圆. 设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA,PD,PB,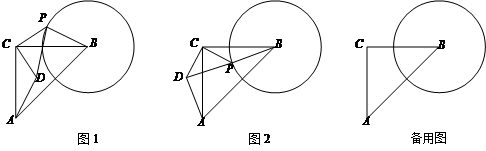
(1)求证:AD=BP;
(2)若DP与⊙B相切,则∠CPB的度数为_________°;
(3)如图2,当B,P,D三点在同一直线上时,求BD的长;
(4)BD的最小值为________,此时tan∠CBP=_________;BD的最大值为 ,此时tan∠CPB=_________.
(本小题满分13分)
某公司经销农产品业务,以3万元/吨的价格向农户收购农产品后,以甲、乙两种方式进行销售,甲方式包装后直接销售;乙方式深加工后再销售.甲方式农产品的包装成本为1万元/吨,根据市场调查,它每吨平均销售价格y(单位:万元)与销售量m(单位:吨)之间的函数关系为y = -m+14(2≤m≤8);乙方式农产品深加工等(不含进价)总费用S(单位:万元)与销售量n(单位:吨)之间的函数关系是S=3n+12,平均销售价格为9万元/吨.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(- ,
, )
)
(1)该公司收购了20吨农产品,其中甲方式销售农产品x吨,其余农产品用乙方式销售,经销这20吨农产品所获得的毛利润为w万元(毛利润=销售总收入-经营总成本).
①直接写出:甲方式购买和包装x吨农产品所需资金为_________万元;乙方式购买和加工其余农产品所需资金为_________万元;
②求出w关于x的函数关系式;
③若农产品全部销售该公司共获得了48万元毛利润,求x的值;
④若农产品全部售出,该公司的最小利润是多少.
(2)该公司现有流动资金132万元,若将现有流动资金全部用于经销农产品,
①其中甲方式经销农产品x吨,则总经销量p为__________吨(用含x的代数式表示);
②当x为何值时,使公司获得最大毛利润,并求出最大毛利润.
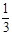

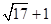 的值在( )
的值在( )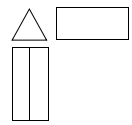
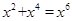
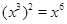
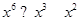





 =
= 的解为( )
的解为( )

 -4x+2= .
-4x+2= . 和
和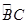 都经过圆心O,则阴影部分的面积是 (结果保留π)
都经过圆心O,则阴影部分的面积是 (结果保留π)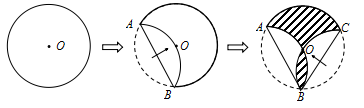
 粤公网安备 44130202000953号
粤公网安备 44130202000953号