(本小题满分11分)如图1,在△ABC中,∠ACB=90°,AC=BC= ,以点B为圆心,以1为半径作圆. 设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA,PD,PB,
,以点B为圆心,以1为半径作圆. 设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA,PD,PB,
(1)求证:AD=BP;
(2)若DP与⊙B相切,则∠CPB的度数为_________°;
(3)如图2,当B,P,D三点在同一直线上时,求BD的长;
(4)BD的最小值为________,此时tan∠CBP=_________;BD的最大值为 ,此时tan∠CPB=_________.
相关知识点
推荐套卷
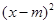 -(x-m),其中m是常数.
-(x-m),其中m是常数.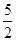
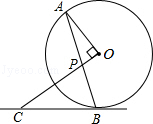
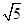 ,OP=1,求BC的长.
,OP=1,求BC的长.
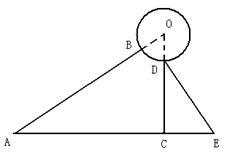
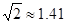 ,
, )
) 粤公网安备 44130202000953号
粤公网安备 44130202000953号