[重庆]2013年重庆市育才成功学校中考一模数学试卷
下列调查中,适合用全面调查方式的是( )
| A.了解一批灯泡的使用寿命 | B.了解一批炮弹的杀伤半径 |
| C.了解某班学生50米跑的成绩 | D.了解一批袋装食品是否含有防腐剂 |
甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好是9.4环,方差分别是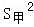 =0.90,
=0.90,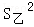 =1.22,
=1.22, =0.43,
=0.43, =1.68,在本次射击测试中,成绩最稳定的是( )
=1.68,在本次射击测试中,成绩最稳定的是( )
| A.甲 | B.乙 |
| C.丙 | D.丁 |
若⊙O1,⊙O2的半径分别是r1=5,r2=3,圆心距d=8,则这两个圆的位置关系是( )
| A.内切 | B.相交 | C.外切 | D.外离 |
点(﹣1,y1),(2,y2),(3,y3)均在函数 的图象上,则y1,y2,y3的大小关系是( )
的图象上,则y1,y2,y3的大小关系是( )
| A.y3<y2<y1 | B.y2<y3<y1 | C.y1<y2<y3 | D.y1<y3<y2 |
如图,矩形ABCD中,P为CD中点,点Q为AB上的动点(不与A,B重合).过Q作QM⊥PA于M,QN⊥PB于N.设AQ的长度为x,QM与QN的长度和为y.则能表示y与x之间的函数关系的图象大致是( )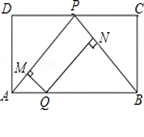

A. B. C. D.
下列矩形都是由大小不等的正方形按照一定规律组成,其中,第①个矩形的周长为6,第②个矩形的周长为10,第③个矩形的周长为16,…则第⑥个矩形的周长为( )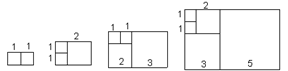
① ② ③ ④
| A.42 | B.46 | C.68 | D.72 |
据重庆市统计局公布的数据,今年一季度全市实现国民生产总值约为7840000万元.那么7840000万元用科学记数法表示为 万元.
自3月1日新“国五条”细则出台,三周以来我市二手房交易市场持续火爆。根据我市网上房地产数据显示,我市二手住宅成交量连续三周环比上涨,成交套数分别为1175套、1587套和1735套。而细则出台前一周,我市二手住宅成交量仅为249套。这四周我市二手住宅成交量的极差是 套;
如图,AB、AC是⊙O的弦,OE⊥AB、OF⊥AC,垂足分别为E、F.如果EF=3.5,那么BC= _____ .
如图所示,在4×4的方格中每个小正方形的边长是单位1,小正方形的顶点称为格点。现有格点A、B,在方格中任意找一点C(必须是格点),使△ABC成为等腰三角形的概率是 
重庆市政府为了大力发展农牧业,鼓励并支持青年自主创业。打工返乡青年甲、乙两人在政府帮助下合伙养了若干头羊,而每头羊的卖价又恰与羊的头数相等,全部卖完后,两人按下面的方法平分钱:先由甲拿十元,再由乙拿十元,如此轮流,拿到最后,剩下不足十元(都是整元),轮到乙拿去.为了平均分配,甲应该找补给乙 元?
如图所示,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到 ,再将
,再将 绕点
绕点 顺时针旋转90°得到
顺时针旋转90°得到 。
。
(1)作出 和
和 ;
;
(2)直接写出 旋转时绕过的面积。
旋转时绕过的面积。
某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
2012年5月31日是世界卫生组织发起的第25个“世界无烟日” .重庆育才成功学校学生处鼓励学生积极宣传,并设计调查问卷,以更好地宣传吸烟的危害.八年级十一班数学兴趣小组第一组的5名同学设计了如下调查问卷,随机调查了部分吸烟人群,并将调查结果绘制成统计图.

根据以上信息,解答下列问题:
(1)本次接受调查的总人数是 人,并把条形统计图补充完整.
(2)在扇形统计图中,C选项的人数所占百分比是 ,E选项所在扇形的圆心角的度数是 .
(3)重庆育才成功学校八年级十一班数学兴趣小组第一组的5名同学中有两名男同学,学校学生处准备从八年级十一班数学兴趣小组第一组的5名同学中选取两名同学参加“世界无烟日”活动的总结会,请你用列表法或画树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
如图,E为正方形 的CD边上一点,连接BE,过点A作AF∥BE,交CD的延长线于点F,
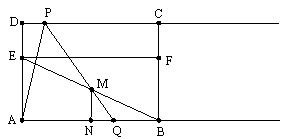
的CD边上一点,连接BE,过点A作AF∥BE,交CD的延长线于点F, 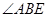 的平分线分别交AF、AD于点G、H.
的平分线分别交AF、AD于点G、H.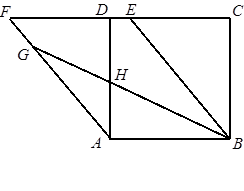
(1)若 ,
,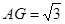 ,求
,求 的长度;
的长度;
(2)证明: .
.
已知: 是方程
是方程 的两个实数根,且
的两个实数根,且 ,抛物线
,抛物线 的图像经过点A(
的图像经过点A( )、B(
)、B( ).
).
(1)求这个抛物线的解析式;
(2) 设(1)中抛物线与 轴的另一交点为C,抛物线的顶点为D,
轴的另一交点为C,抛物线的顶点为D,
试求出点C、D的坐标和△BCD的面积;
(3) P是线段OC上的一点,过点P作PH⊥ 轴,与抛物线交于H点,
轴,与抛物线交于H点,
若直线BC把△PCH分成面积之比为2:3的两部分,请求出P点的坐标.
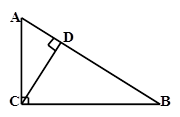
如图,在矩形ABCD中,AB=6,AD= ,点E是AD的三等分点,且AE
,点E是AD的三等分点,且AE DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为
DE,过点E作EF∥AB交BC于F,并作射线DC和AB,点P、Q分别是射线DC和射线AB上动点,点P以每秒1个单位的速度向右平移,且始终满足∠PQA=60°,设P点运动的时间为 .
.
(1)当点Q与点B重合时,求DP的长度;
(2)设AB的中点为N,PQ与线段BE相交于点M,是否存在点P,使△ 为等腰三角形?若存在,请直接写出时间
为等腰三角形?若存在,请直接写出时间 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)设△ 与四边形
与四边形 的重叠部分的面积为S,试求S与
的重叠部分的面积为S,试求S与 的函数关系式和相应的自变量
的函数关系式和相应的自变量 的取值范围.
的取值范围.
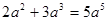

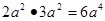
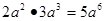


 =( )
=( )
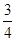
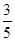
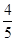
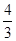
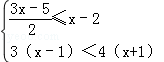 的解集是( )
的解集是( )
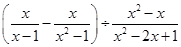 ,其中
,其中 是不等式组
是不等式组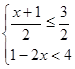 的整数解.
的整数解. 粤公网安备 44130202000953号
粤公网安备 44130202000953号