江苏省无锡市南长区九年级上学期期中考试数学试卷
方程x2-2x=0的根是( )
| A.x1=0,x2=2 | B.x1=0,x2=-2 | C.x=0 | D.x=2 |
下列一元二次方程中,有实数根的是 ( )
| A.x2-x+1=0 | B.x2-2x+3=0 | C.x2+x-1=0 | D.x2+4=0 |
若△ABC∽△A'B'C',∠A=40°,∠C=110°,则∠B'的度数为 ( )
| A.30° | B.50° | C.40° | D.70° |
如图,等边△ABC的边长为2,DE是它的中位线,则下列三个结论:①DE=1;②△CDE∽△CAB;③△CDE与△CAB的面积之比为1:4.其中正确的有 ( )
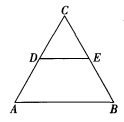
| A.0个 | B.1个 | C.2个 | D.3个 |
如图,在一幅长80cm,宽50 cm的矩形树叶画四周镶一条金色的纸边,制成一幅矩形挂图,若要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,则满足的方程是( )

| A.(80+x)(50+x)=5400 |
| B.(80+2x)(50+2x)=5400 |
| C.(80+2x)(50+x)=5400 |
| D.(80+x)(50+2x)=5400 |
已知m,n是方程x2-x-2016=0的两个实数根,则m2+n的值为于( )
| A.1008 | B.2015 | C.2016 | D.2017 |
以下命题:①直径相等的圆是等圆;②长度相等弧是等弧;③一个圆只有一条直径;④直径是圆中最长的弦.其中正确的个数是( )
| A.1 | B.2 | C.3 | D.4 |
如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为 ⊙O的直径,AB=3,则AD的值为( )
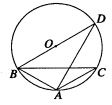
| A.6 | B.3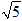 |
C.3 | D.3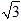 |
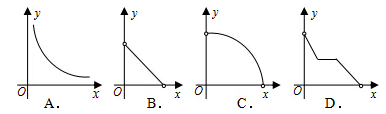
如图,△ABC中,AB=AC=2,∠BAC=20°,动点P、Q分别在直线BC上运动,且始终保持∠PAQ=100°.设BP=x,CQ=y,则y与x之间的函数关系用图象大致可表示为( )

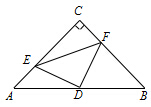
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在运动变化过程中,下列结论:①△DFE是等腰直角三角形;②四边形CEDF不可能为正方形;③四边形CEDF的面积随点E位置的改变而发生变化;④点C、E、D、F四点在同一个圆上,且该圆面积最小为4π;⑤DE•DF+CE•CF的值是定值为8,其中正确结论的个数是( )
A.4 B.3 C.2 D.1
如图,线段AB两个端点坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则点D的坐标为 .
后得到线段CD,则点D的坐标为 .

如图,在△ABC中,以AC边为直径的⊙O交BC于点D,过点B作BG⊥AC交⊙O于点E、H,连AD、ED、EC,若BD=8,DC=6,则CE的长为 .

在直角坐标系中,点A1的坐标为(1,0),过点A1作x轴的垂线交直线y=2x于A2,过点A2作直线y=2x的垂线交x轴于A3,过点A3作x轴的垂线交直线y=2x于A4,依此规律,则A2016的坐标为 .

关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(2)如果△ABC是等边三角形,试求这个一元二次方程的根.
(1)如图①,用尺规作图作出圆的一条直径EF(不写作法,保留作图痕迹);
(2)如图②,A、B、C、D为圆上四点,AB∥CD,AB<CD,请只用无刻度的直尺,画出圆的一条直径EF(不写画法,保留画图痕迹).
如图,在矩形ABCD中, CF⊥BD分别交BD、AD于点E、F.
(1)求证:△DEC ∽ △FDC;
(2)若DE=2 ,F为AD的中点,求BD的长度.
,F为AD的中点,求BD的长度.
如图,AC是⊙O的直径,PB切⊙O于点D,交AC的延长线于点B,且∠DAB=∠B.
(1)求∠B的度数;
(2)若BD=9,求BC的长.
在“文化南长•全民阅读”活动中,某中学社团“清风读书社”对全校学生的人数及纸质图书阅读量(单位:本)进行了调查.2014年全校有1000名学生,2015年全校学生人数比2014年增加10%,2016年全校学生人数比2015年增加100人.
(1)2016年全校学生有 人;
(2)2015年全校学生人均阅读量比2014年多1本,阅读总量比2014年增加1700本.
(注:阅读总量=人均阅读量×人数)
①求2014年全校学生人均阅读量;
②2014年读书社人均阅读量是全校学生人均阅读量的2.5倍,如果2015年、2016年这两年读书社人均阅读量都比前一年增长一个相同的百分数a,2016年全校学生人均阅读量比2014年增加的百分数也是a,那么2016年读书社全部80名成员的阅读总量将达到全校学生阅读总量的25%,求a的值.
我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,点C是⊙O上一点(不与点A,B重合),D是半圆  的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
求证:△ACE是奇异三角形.
 =
= ,则
,则 = .
= .




 +
+ 的值是否为定值?若是,求出定值;若不是,请说明理由.
的值是否为定值?若是,求出定值;若不是,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号