在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.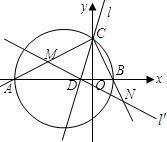
(1)求点C的坐标;
(2)若∠ACB的平分线所在的直线l交x轴于点D,求直线l对应的一次函数关系式;
(3)过点D任作一直线l′分别交射线CA、CB(点C除外)于点M、N,则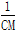 +
+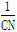 的值是否为定值?若是,求出定值;若不是,请说明理由.
的值是否为定值?若是,求出定值;若不是,请说明理由.
推荐套卷
在平面直角坐标系中,△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆与y轴正半轴交于点C,A、B两点的横坐标xA、xB是关于x的方程x2+3x-4=0的两个根.
(1)求点C的坐标;
(2)若∠ACB的平分线所在的直线l交x轴于点D,求直线l对应的一次函数关系式;
(3)过点D任作一直线l′分别交射线CA、CB(点C除外)于点M、N,则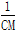 +
+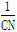 的值是否为定值?若是,求出定值;若不是,请说明理由.
的值是否为定值?若是,求出定值;若不是,请说明理由.