我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,点C是⊙O上一点(不与点A,B重合),D是半圆  的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
求证:△ACE是奇异三角形.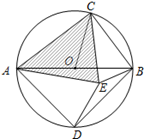
推荐套卷
我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,点C是⊙O上一点(不与点A,B重合),D是半圆  的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
求证:△ACE是奇异三角形.