初中数学一次函数的最值解答题

如图是某汽车行驶的路程S(km)与时间t(分钟) 的函数关系图.观察图中所提供的信息,解答下列问题

（1）汽车在前9分钟内的平均速度是       km/分；
（2）汽车在中途停了多长时间?       ；
（3）当16≤t≤30时,求S与t的函数关系式.

某电子厂商投产一种新型电子产品，每件制造成本为18元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y=﹣2x+100．（利润=售价﹣制造成本）
（1）写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；
（2）当销售单价为多少元时，厂商每月能获得350万元的利润？当销售单价为多少元时，厂商每月能获得最大利润？最大利润是多少？
（3）根据相关部门规定，这种电子产品的销售单价不能高于32元，如果厂商要获得每月不低于350万元的利润，那么制造出这种产品每月的最低制造成本需要多少万元？

小明从家骑自行车出发，沿一条直路到相距2400m的邮局办事，小明出发的同时，他的爸爸以96m/min速度从邮局同一条道路步行回家，小明在邮局停留2min后沿原路以原速返回，设他们出发后经过t min时，小明与家之间的距离为s₁ m，小明爸爸与家之间的距离为s₂ m，图中折线OABD、线段EF分别表示s₁、s₂与t之间的函数关系的图象．

（1）求s₂与t之间的函数关系式；
（2）小明从家出发，经过多长时间在返回途中追上爸爸？这时他们距离家还有多远？

已知一次函数y=kx+b的图象是过A（0，-4），B（2，-3）两点的一条直线．
（1）求直线AB的解析式；
（2）将直线AB向左平移6个单位，求平移后的直线的解析式．
（3）将直线AB向上平移6个单位，求原点到平移后的直线的距离．

如图，直线l₁的解析表达式为：y=-3x+3，且l₁与x轴交于点D，直线l₂经过点A，B，直线l₁，l₂交于点C．

（1）求点D的坐标；
（2）求直线l₂的解析表达式；
（3）求△ADC的面积；
（4）在直线l₂上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．

为表彰在“深圳读书月”活动中表现积极的同学，某班级决定购买文具盒与钢笔作为奖品.已知3个文具盒、2支钢笔共需72元；1个文具盒、2支钢笔共需44元.
（1）每个文具盒、每支钢笔各多少元？
（2）时逢“元旦”，商店举行优惠促销活动，具体办法如下：文具盒九折，钢笔10支以上超出部分八折.设买x₁个文具盒需要y₁元，买x₂支钢笔需要y₂元，求y₁、y₂关于x的函数关系式，并写出自变量的取值范围.

已知：一次函数y=kx+b的图象经过M（0，2），N（1，3）两点.
求：
（1）图象与x轴的交点坐标；
（2）图象与两坐标轴围成的三角形面积.

如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点M在线段OA和射线AC上运动．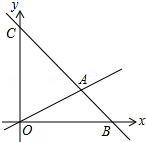

（1）求直线AB的解析式．
（2）求△OAC的面积．
（3）是否存在点M，使△OMC的面积是△OAC的面积的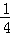？若存在求出此时点M的坐标；若不存在，说明理由．

为加强与家长的沟通，某校在家长会到来之前需印刷《致家长的一封信》等材料以作宣传，该校的印刷任务原来由甲复印店承接，其收费y（元）与印刷页数x（页）的函数关系如图所示．

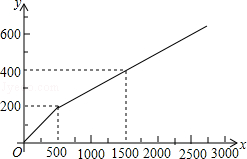
（1）从图象中可看出：印刷超过500页部分每页收费     元；
（2）现在乙印刷厂表示：每页0.15元收费．另收200元的制版费，乙印刷厂收费y（元）与印刷页数x（页）的函数关系为        ；
（3）在给出的坐标系内画出（2）中的函数图象，并结合函数图象回答印刷页数在3000页左右应选择哪个印刷店？

如图，请根据图象所提供的信息解答下列问题：

（1）当x   时，kx+b≥mx-n；
（2）不等式kx+b＜0的解集是               ；
（3）交点P的坐标（1，1）是一元二次方程组：           的解；
（4）若直线l₁分别交x轴、y轴于点M、A，直线l₂分别交x轴、y轴于点B、N，求点M的坐标和四边形OMPN的面积．

关于x的一次函数y=mx﹣2n与反比例函数的图象的一个交点A（1，﹣4），求一次函数和反比例函数的解析式．

如图，直线y=﹣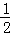x+b交x轴于点A，交直线y=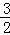x于点B（2，m），矩形CDEF的边DC在x轴上，D在C的左侧，EF在x轴的上方，DC=2，DE=4．当点C的坐标为（﹣2，0）时，矩形CDEF开始以每秒2个单位的速度沿x轴向右运动，运动时间为t秒．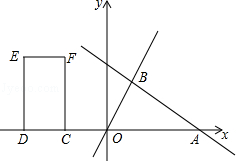

（1）求b，m的值；
（2）矩形CDEF运动t秒时，直接写出C、D两点的坐标（用含t的代数式表示）；
（3）当点B在矩形CDEF的一边上时，求t的值．

如图1，在一次航海模型船训练中，A₁B₁和A₂B₂是水面上相邻的两条赛道（看成两条互相平行的线段）．甲船在赛道A₁B₁上从A₁处出发，到达B₁后，以同样的速度返回A₁处，然后重复上述过程；乙船在赛道A₂B₂上以2m/s的速度从B₂处出发，到达A₂后以相同的速度回到B₂处，然后重复上述过程（不考虑每次折返时的减速和转向时间）．若甲、乙两船同时出发，设离开池边B₁B₂的距离为y（m），运动时间为t（s），甲船运动时，y（m）与t（s）的函数图象如图2所示．

（1）赛道的长度是         m，甲船的速度是         m/s；
（2）分别求出甲船在0≤t≤30和30＜t≤60时，y关于t的函数关系式；
（3）求出乙船由B₂到达A₂的时间，并在图2中画出乙船在3 分钟内的函数图象；
（4）请你根据（3）中所画的图象直接判断，若从甲、乙两船同时开始出发到3分钟为止，甲、乙共相遇了几次？

将长为20cm，宽为10cm的长方形白纸，按如图所示的方法粘贴起来，粘合部分的宽为2cm．设x张白纸粘合后的纸条总长度为ycm，

（1）求y与x之间的函数关系式，并画出函数图象，
（2）若x=20，求纸条的面积．

暑假期间，小明和父母一起开车到距家200千米的景点旅游．出发前，汽车油箱内储油45升；当行驶150千米时，发现油箱剩余油量为30升．
（1）已知油箱内余油量y（升）是行驶路程x（千米）的一次函数，求y与x的函数关系式；
（2）当油箱中余油量少于3升时，汽车将自动报警．如果往返途中不加油，他们能否在汽车报警前回到家？请说明理由．