初中数学一次函数的最值解答题

已知:正比例函数y=（m﹣1）的图象在第二、四象限，求m的值．

将正比例函数y=2x的图象沿y轴平移后，恰好经过点A（2，3），求平移后的函数解析式．

某商场欲购进果汁饮料和碳酸饮料共50箱，两种饮料每箱的进价和售价如下表所示．设购进果汁饮料x箱（x为正整数），且所购进的两种饮料能全部卖出，获得的总利润为W元（注：总利润=总售价﹣总进价）．
（1）设商场购进碳酸饮料y箱，直接写出y与x的函数关系式；
（2）求总利润w关于x的函数关系式；
（3）如果购进两种饮料的总费用不超过2100元，那么该商场如何进货才能获利最多？并求出最大利润．
饮料 果汁饮料 碳酸饮料
进价（元/箱） 51 36
售价（元/箱） 61 43

如图，直线l₁的解析式为y=﹣3x+3，且l₁与x轴交于点D，直线l₂经过点A，B，直线l₁，l₂交于点C．

（1）求直线l₂的解析表达式；
（2）求△ADC的面积；
（3）若点P为第一象限上的一点，且以A，C，D，P为顶点的四边形为平行四边形，试求点P的坐标．

某工厂生产一种产品，当生产数量至少为10吨，但不超过50吨时，每吨的成本y（万元/吨）与生产数量x（吨）的函数关系式如图所示．

（1）求y关于x的函数解析式，并写出自变量的取值范围；
（2）当每吨成本为9万元时，求该产品的生产数量．

已知直线y=x+b经过点P（4，﹣1），当y＜0时，求x的取值范围．

已知平行四边形ABCD位置在平面直角坐标系中如图1所示，BC=AC，且OA=6，OC=8．

（1）求点D的坐标；
（2）动点P从点C出发，以每秒1个单位的速度沿线段以向终点A运动，动点Q从点A出发以每秒2个单位的速度沿4射线AD运动，两点同时出发，当P到达终点时，点Q停止运动，在运动过程中，过点Q作MQ∥AB交射线AC于M（如图2）．设PM=y，运动时间为t（t＞0），求y与t的函数关系式，并直接写出自变量的取值范围；
（3）在（（2）的条件下，作点P关于直线CD的对称点P′（如图3），当P′D=时，求运动时间t．

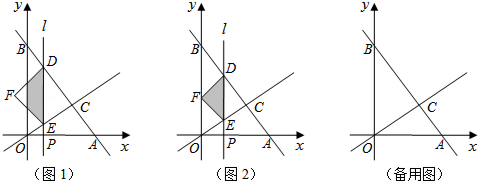
如图1，直线y=﹣x+b分别与x轴、y轴交于A、B两点，与直线y=kx交于点C（2，）．平行于y轴的直线l从原点O出发，以每秒1个单位长度的速度沿x轴向右平移，到C点时停止；直线l分别交线段BC、OC、x轴于点D、E、P，以DE为斜边向左侧作等腰直角△DEF，设直线l的运动时间为t（秒）．

（1）填空：k=  ；b=  ；
（2）当t为何值时，点F在y轴上（如图2所示）；
（3）设△DEF与△BCO重叠部分的面积为S，请直接写出S与t的函数关系式（不要求写解答过程），并写出t的取值范围．

如图，一次函数y=k₁x+b的图象与反比例函数y=的图象交于A（1，4），B（3，m）两点，

（1）求一次函数和反比例函数的表达式；
（2）求△AOB的面积．

如图，A（0，1），M（3，2），N（4，4）．动点P从点A出发，沿y轴以每秒1个单位长的速度向上移动，且过点P的直线l：y=﹣x+b也随之移动，设移动时间为t秒．

（1）当t=3时，求直线的解析式；
（2）当直线通过点M时，求直线l的解析式；
（3）若点M，N位于l的异侧，确定t的取值范围．

甲、乙两人沿相同的路线由A到B匀速行进，A、B两地间的路程为16km，他们行进的路程s（km）与甲出发后的时间t（h）之间的函数图象如图所示，则下列判断错误的是（ ）

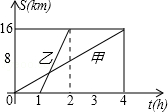
A.乙比甲晚出发1h  B.甲比乙晚到B地2h
C.甲的速度是4km/h D.乙的速度是8km/h

甲市火车货运站现有苹果1530吨，梨1150吨，安排一列货车将这批苹果和梨运往乙市．这列货车可以挂A、B两种不同规格的货箱共50节，已知用一节A型货箱的运费是0.5万元，用一节B型货箱的运费用是.0.8万元．
（1）设运输这批苹果和梨的总运费为y（万元），用A型货箱的节数为x（节），试写出y与x的函数关系式．
（2）已知35吨苹果和15吨梨可装满一节A型货箱，25吨苹果和35吨梨可装满一节B型车箱，请问运输所有苹果和梨的方案共有几种，请设计出来．
（3）利用函数的性质说明，在第（2）问的方案中，哪种方案的运费最少，最少运费用是多少？

如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，AC，OD交于点P，其中OA=4，OB=3．

（1）求OD所在直线的解析式；
（2）求△AOP的面积．

已知水银体温计的读数y（℃）与水银柱的长度x（cm）之间是一次函数关系．现有一支水银体温计，其部分刻度线不清晰（如图），表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度．

水银柱的长度x（cm） 4.2 … 8.2 9.8
体温计的读数y（℃） 35.0 … 40.0 42.0
（1）求y关于x的函数关系式（不需要写出函数的定义域）；
（2）用该体温计测体温时，水银柱的长度为6.2cm，求此时体温计的读数．

如图，已知两直线l₁和l₂相交于点A（4，3），且OA=OB，

（1）分别求出两条直线对应的函数解析式．
（2）当x为何值时，一次函数l₁的函数值大于l₂的函数值？