已知2y﹣3与﹣3x﹣1成正比例，且x=2时，y=5．
（1）求y与x之间的函数关系式，并在坐标系中画出图象；
（2）若﹣1≤y≤2，求x的取值范围；
（3）若把直线向下平移3个单位长度，那么平移后的直线的解析式为 ，请画出图象．
已知一个一次函数的图象与一个反比例函数的图象交于点P（﹣2，1）、Q（1，m）．
（1）分别求出这两个函数的表达式．
（2）在同一平面直角坐标系中画出这两个函数的图象，根据图象回答，当x取何值时，一次函数的值大于反比例函数的值？
如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．
（1）求直线AB的解析式；
（2）若直线AB上的点C在第一象限，且S△BOC=2，求点C的坐标．
一次函数y=kx+4的图象经过点A（﹣3，﹣2）．
（1）求这个一次函数的关系式；
（2）判断点B（﹣5，3）是否在这个函数的图象上．
星期天，玲玲骑自行车到郊外游玩，她离家的距离与时间的关系如图所示，请根据图象回答下列问题．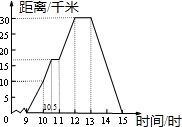
（1）玲玲到达离家最远的地方需要多长时间？离家多远？
（2）她何时开始第一次休息？休息了多长时间？
（3）她骑车速度最快是在什么时候？车速多少？
（4）玲玲全程骑车的平均速度是多少？
在平面直角坐标系xOy中，点A（0，4），B（3，0），以AB为边在第一象限内作正方形ABCD，直线l：y=kx+3．
（1）当直线l经过D点时，求点D的坐标及k的值；
（2）当直线l与正方形有两个交点时，直接写出k的取值范围．
如图，是某工程队在“村村通”工程中修筑的公路长度y（米）与时间x（天）（其中0≤x≤8）之间的关系图象．根据图象提供的信息，求该公路的长．
一次函数y=kx+b（k≠0）的图象经过点（1，﹣3），且与y=2x平行，求这个一次函数表达式．
如图，直线y=kx+b经过点A（5，0），B（1，4）。
（1）求直线AB的解析式；
（2）若直线y=2x-4与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式2x-4>kx+b的解集。
甲、乙两车从A地前往B地，甲车行至AB的中点C处后，以原来速度的1.5倍继续行驶，在整个行程中，汽车离开A地的距离y与时刻t的对应关系如图所示，求：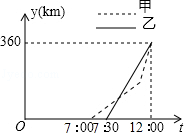
（1）甲车何时到达C地；
（2）甲车离开A地的距离y与时刻t的函数解析式；
（3）乙车出发后何时与甲车相距20km．
如图：直线y=kx+3与x轴、y轴分别交于A、B两点，tan∠OAB=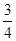
，点C（x，y）是直线y=kx+3上与A、B不重合的动点．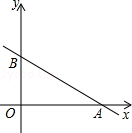
（1）求直线y=kx+3的解析式；
（2）当点C运动到什么位置时△AOC的面积是6；
（3）过点C的另一直线CD与y轴相交于D点，是否存在点C使△BCD与△AOB全等？若存在，请求出点C的坐标；若不存在，请说明理由．
我校实行学案教学，需印刷若干份数学学案．印刷厂有甲、乙两种收费方式，除按印数收取印刷费外，甲种方式还需收取制版费而乙种不需要．两种印刷方式的费用y（元）与印刷份数x（份）之间的关系如图所示：
（1）填空：
甲种收费方式的函数关系式是y1= ；
乙种收费方式的函数关系式是y2= ；
（2）如果我校2014-2015学年八年级每次印刷100～450（含100和450）份学案，选择哪种印刷方式较合算．
如图，已知直线y=3x+3与x轴交于点A，与y轴交于点D，与直线y=
x交于点E．过点D作DC∥x轴，交直线y=x于点C，过点C作CB∥AD交x轴于点B．
（1）点C的坐标是 ；
（2）以线段AD的中点M为圆心作⊙M，当⊙M与直线CE相切时，求⊙M的半径；
（3）如图2，点P从点O出发，沿线段OC向终点C运动，点Q从点C出发，沿线段CD向终点D运动．若P、Q两点同时出发，速度均为1单位长度/s，时间为t/s．当p、q两点有一点到达终点时，它们均停止运动．将线段PQ绕点P沿顺时针方向旋转90°．当点Q落在四边形ABCD一边所在的直线上时，t的值为 ．
在“五•一”期间，“佳佳”网店购进A、B两种品牌的服装进行销售，已知B种品牌服装的进价比A种品牌服装的进价每件高20元，2件A种品牌服装与3件B种品牌服装进价共560元．
（1）求购进A、B两种品牌服 装的单价；
（2）该网站拟以不超过11200元的总价购进这种两品牌服装共100件，并全部售出．其中A种品牌服装的售价为150元/件，B种品牌服装的售价为200元/件，该网站为了获取最大利润，应分别购进A、B两种品牌服装各多少件？所获取的最大利润是多少？
如图，点A（2，2）在双曲线y1=
（x＞0）上，点C在双曲线y2=－
（x＜0）上，分别过A、C向x轴作垂线，垂足分别为F、E，以A、C为顶点作正方形ABCD，且使点B在x轴上，点D在y轴的正半轴上．
（1）求k的值；
（2）求证：△BCE≌△ABF；
（3）求直线BD的解析式．
粤公网安备 44130202000953号
