初中数学一次函数的最值解答题

一个安装了两个进水管和一个出水管的容器，每分钟的进水量和出水量是两个常数，且两个进水管的进水速度相同．进水管和出水管的进出水速度如图1所示，某时刻开始到6分钟（至少打开一个水管），该容器的水量y（单位：升）与时间x如图2所示．

（1）试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况．
（2）求4≤x≤6时，y随x变化的函数关系式．
（3）6分钟后，若同时打开两个水管，则10分钟时容器的水量是多少升？

已知点P（x，y）是第一象限内的一个动点，且满足x+y=4．请先在所给的平面直角坐标系中画出函数y=2x+1的图象，该图象与x轴交于点A，然后解答下列问题：

（1）利用所画图象，求当-1≤y≤3时x的取值范围；
（2）若点P正好也在直线y=2x+1上，求点P的坐标；
（3）设△OPA的面积为S，求S关于点P的横坐标x的函数解析式．

如图，A、B两点的坐标分别是A（1，）、B（0，）．

（1）求△OAB的面积；
（2）若过A、B两点的直线解析式为y=kx+b，求k，b的值．（本小题结果保留小数点后一位）

如图，反比例函数y=的图象与一次函数y=ax+b的图象交于点A（1，4），点B（m，﹣2）

（1）求这两个函数的关系式；
（2）观察图象，写出不等式＞ax+b的解集；
（3）如果有一点C与点A关于x轴对称，求△ABC的面积．

为改善生态环境，防止水土流失，某村计划在江汉堤坡种植白杨树，现甲、乙两家林场有相同的白杨树苗可供选择，其具体销售方案如下：

设购买白杨树苗x棵，到两家林场购买所需费用分别为y_甲（元）、y_乙（元）．
（1）该村需要购买1500棵白杨树苗，若都在甲林场购买所需费用为         元，若都在乙林场购买所需费用为         元；
（2）分别求出y_甲、y_乙与x之间的函数关系式；
（3）如果你是该村的负责人，应该选择到哪家林场购买树苗合算，为什么？

如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．

（1）求直线AB的解析式；
（2）若直线AB上的点C在第一象限，且S_△BOC=2，求点C的坐标．

在平面直角坐标系中，直线y₁=x+a和y₂=﹣x+b交于点E（3，3），点P（m，n）在直线y₁=x+a上，过点P（m，n）作x轴的垂线，交直线y₂=﹣x+b于点F．
（1）若n=2，求△PEF的面积；
（2）若PF=2，求点P的坐标．

在同一平面直角坐标系中，观察以下直线：y=2x，y=﹣x+6，y=x+2，y=4x﹣4图象的共同特点，若y=kx+5也有该特点，试求满足条件的k值．

某商场筹集资金12.8万元，一次性购进空调、彩电共30台．根据市场需要，这些空调、彩电可以全部销售，全部销售后利润不少于1.5万元，其中空调、彩电的进价和售价见表格．
空调 彩电
进价（元/台） 5400 3500
售价（元/台） 6100 3900
设商场计划购进空调x台，空调和彩电全部销售后商场获得的利润为y元．
（1）试写出y与x的函数关系式；
（2）商场有哪几种进货方案可供选择？
（3）选择哪种进货方案，商场获利最大？最大利润是多少元？

已知：在平面直角坐标系中，点A（1，0），点B（4，0），点C在y轴正半轴上，且OB=2OC．
（1）试确定直线BC的解析式；
（2）在平面内确定点M，使得以点M、A、B、C为顶点的四边形是平行四边形，请直接写出点M的坐标．

（1）某水果批发商，批发苹果不少于80kg时，批发价为2.5元/kg，小张携现金2500元到这个市场采购苹果，并以批发价买进，设购买的苹果为xkg，小张付款后还剩余现金y元，写出y与x的函数关系式，并指出自变量x的取值范围．
（2）在直角坐标系中，直接画出函数y=|x+1|的图象．

如图，在平面直角坐标系中，一次函数的图象经过点A（6，﹣3）和点B（﹣2，5）．

（1）求这个一次函数的表达式．
（2）判断点C（﹣1，4）是否在该函数图象上．

甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地，如图，是它们离甲地距离y（千米）与时间x（小时）之间的函数关系图象，请根据图象解答下列问题：

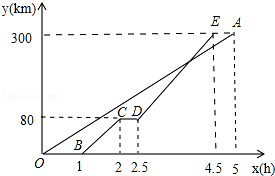
（1）线段CD表示轿车在途中停留了          小时；
（2）直线OA和直线DE的交点坐标可以看做方程组           的解．

如图，一次函数y=﹣x+m的图象和y轴交于点B，与正比例函数y=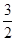x图象交于点P（2，n）．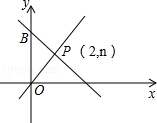

（1）求m和n的值；
（2）求△POB的面积．

某零件制造厂有工人20名，已知每名工人每天可制造甲种零件6个或乙种零件5个，且每制造一个甲种零件的成本为400元，可获利150元，每制造一个乙种零件的成本为500元，可获利260元．在这20名工人中，车间每天安排x名工人制造甲种零件，其余工人制造乙种零件．
（1）写出次厂家每天获利y（元）与x（元）之间的函数关系式；
（2）若该厂家每天最多能投入的成本为49000元，那么该厂家每天最多能获利多少元？