如图，请根据图象所提供的信息解答下列问题：
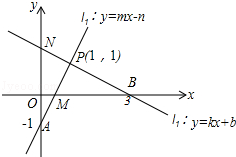
（1）当x 时，kx+b≥mx-n；
（2）不等式kx+b＜0的解集是 ；
（3）交点P的坐标（1，1）是一元二次方程组： 的解；
（4）若直线l1分别交x轴、y轴于点M、A，直线l2分别交x轴、y轴于点B、N，求点M的坐标和四边形OMPN的面积．
相关试题
与-0.76；（2）-
与-
；
与-3
与-│-
│；（4）-
与-│3.14│．
，b=-
，试比较a，b的大小．
与-0.626363．推荐套卷
如图，请根据图象所提供的信息解答下列问题：
（1）当x 时，kx+b≥mx-n；
（2）不等式kx+b＜0的解集是 ；
（3）交点P的坐标（1，1）是一元二次方程组： 的解；
（4）若直线l1分别交x轴、y轴于点M、A，直线l2分别交x轴、y轴于点B、N，求点M的坐标和四边形OMPN的面积．
粤公网安备 44130202000953号