如图正方形ABCD,其边长为4.P是射线AB上的点,且AP=x.将△APD沿过点D的折痕PD折叠,点A的落点记为A/,若△A/DP与正方形ABCD的重叠面积记为S,
(1)若x="6," 则S= ▲
(2) ≤S≤1时,则x的取值范围为(用含x的不等式表示)____▲ ______.
≤S≤1时,则x的取值范围为(用含x的不等式表示)____▲ ______.
老师给出一个y关于x的函数,甲、乙、丙、丁四位同学各指出这个函数的一个性质:甲:函数图象不经过第三象限;乙:函数图象经过第一象限;丙:当x<2时,y随x的增大而减小;丁:当x<2时y>0.已知这四位同学叙述都正确。请写出满足上述所有性质的一个函数______________.
请写出一个以直线 为对称轴,且在对称轴右侧部分是下降的抛物线的表
为对称轴,且在对称轴右侧部分是下降的抛物线的表
达式,这条抛物线的表达式可以是 .
将二次函数y=(x﹣2)2+3的图象向右平移2个单位,再向下平移2个单位,所得二次函数的解析式为 . .
在同一平面内下列4个函数;①y=2(x+1)2﹣1;②y=2x2+3;③y=﹣2x2﹣1;④ 的图象不可能由函数y=2x2+1的图象通过平移变换得到
的图象不可能由函数y=2x2+1的图象通过平移变换得到
的函数是 .(把你认为正确的序号都填写在横线上)
(11·大连)如图5,抛物线y=-x2+2x+m(m<0)与x轴相交于点A(x1,0)、B(x2,0),点A在点B的左侧.当x=x2-2时,y______0(填“>”“=”或“<”号).
如图,点C是⊙O优弧ACB上的中点,弦AB=6cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向响点B匀速运动,若y=AE²-EF²,则y与动点F的运动时间x(0≤x≤6 )秒的函数关系式为 .
如图,一次函数y=-2x的图象与二次函数y=-x2+3x图象的对称轴交于点B.
(1)写出点B的坐标 ▲ ;
(2)已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于C、D两点. 若以CD为直角边的△PCD与△OCD相似,则点P的坐标为 ▲ .
(11·湖州)如图,已知抛物线 经过点(0,-3),请你确定一个
经过点(0,-3),请你确定一个
b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间。你确定的b的值是▲。
出售某种手工艺品,若每个获利x元,一天可售出 个,则当x=_________元,一天出售该种手工艺品的总利润y最大.
个,则当x=_________元,一天出售该种手工艺品的总利润y最大.
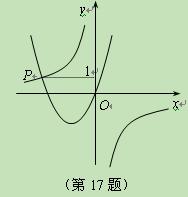
如图,已知函数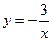 与
与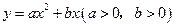 的图象交于点
的图象交于点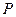 ,点
,点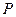 的纵坐标为1,则关于
的纵坐标为1,则关于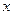 的方程
的方程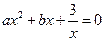 的解为_____________.
的解为_____________.