初中数学二次函数在给定区间上的最值解答题

如图，在平面直角坐标系中，将一块腰长为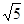的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，顶点A的坐标为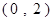，点B在抛物线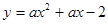上．

（1）直角顶点C的坐标为           ；
（2）求抛物线的解析式；
（3）若点D是（1）中所求抛物线在第三象限内的一个动点，连接BD、CD．当△BCD的面积最大时，求点D的坐标．

如图，抛物线y=ax²+bx+c（a≠0）与x轴交于点A（﹣1，0），B（3，0）两点，与y轴交于点C（0，﹣3）．

（1）求该抛物线的解析式及顶点M坐标；
（2）求△BCM面积与△ABC面积的比；
（3）若P是x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A，P，Q，C为顶点的四边形为平行四边形？若存在，请求出Q点坐标；若不存在，请说明理由．

已知二次函数y=﹣x²+bx+c的图象如图所示，它与x轴的一个交点坐标为A（﹣1，0），另一交点为B，与y轴的交点坐标为C（0，3）．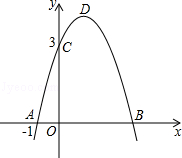

（1）求出b，c的值，并写出此二次函数的解析式；
（2）求出顶点D的坐标以及S_△BCD面积；
（3）根据图象，写出函数值y为正数时，自变量x的取值范围．

为了落实国务院副总理李克强同志到恩施考察时的指示精神，最近，州委州政府又出台了一系列“三农”优惠政策，使农民收入大幅度增加．某农户生产经销一种农副产品，已知这种产品的成本价为20元/千克．市场调查发现，该产品每天的销售量w（千克）与销售价x（元/千克）有如下关系：w=﹣2x+80．设这种产品每天的销售利润为y（元）．
（1）求y与x之间的函数关系式；
（2）当销售价定为多少元时，每天的销售利润最大？最大利润是多少？
（3）如果物价部门规定这种产品的销售价不得高于28元/千克，该农户想要每天获得150元的销售利润，销售价应定为多少元？

已知抛物线．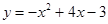
（1）求出这个抛物线的对称轴和顶点坐标；
（2）在给定的坐标系中画出这个抛物线，若抛物线与x轴交于A，B两点，与y轴交于点C，求△ABC的面积．

在一场2015亚洲杯赛B组第二轮比赛中，中国队凭借吴曦和孙可在下半场的两个进球，提前一轮小组出线。如图，足球场上守门员在处开出一高球，球从离地面1米的处飞出（在轴上），运动员孙可在距点6米的处发现球在自己头的正上方达到最高点，距地面约4米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．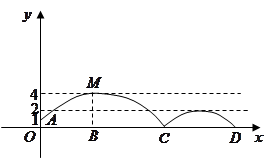

（1）求足球开始飞出到第一次落地时，该抛物线的函数表达式．
（2）足球第一次落地点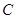距守门员多少米？（取）
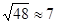（3）孙可要抢到足球第二个落地点，他应从第一次落地点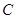再向前跑多少米？（取）

已知二次函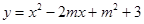数（是常数）．
（1）求证：不论为何值，该函数的图象与x轴没有公共点；
（2）把该函数的图象沿轴向下平移多少个单位长度后，得到的函数的图象与轴只有一个公共点？

已知抛物线
（1）该抛物线的对称轴是      ，顶点坐标       ；
（2）选取适当的数据填入下表，并在直角坐标系内描点画出该抛物线的图象；

x	…						…
y	…						…

 
 
（3）若该抛物线上两点A（x₁，y₁），B（x₂，y₂）的横坐标满足x₁＞x₂＞1，试比较y₁与y₂的大小．

如图，抛物线y =-x²+2x+3与x轴交于点A、B，与y轴交于点C，点D是抛物线的顶点，连接BC、BD．

（1）点D的坐标是         ；
（2）在抛物线的对称轴上求一点M，使点M到点A的距离与到点C的距离之和最小，并求出此时点M的坐标．
（3）若点P在x轴上且位于点B右侧，且点P是线段AQ的中点，连接QD，且∠BDQ=45°，求点P坐标（请利用备用图解决问题）．

问题情境
如图，在x轴上有两点A（m，0），B（n，0）（n＞m＞0）．分别过点A，点B作x轴的垂线，交抛物线y=x²于点C、点D．直线OC交直线BD于点E，直线OD交直线AC于点F，点E、点F的纵坐标分别记为y_E，y_F．
特例探究
填空：
当m=1，n=2时，y_E=              ，y_F=                   ；
当m=3，n=5时，y_E=              ，y_F=                   ．
归纳证明
对任意m，n（n＞m＞0），猜想y_E与y_F的大小关系，并证明你的猜想．
拓展应用
（1）若将“抛物线y=x²”改为“抛物线y=ax²（a＞0）”，其他条件不变，请直接写出y_E与y_F的大小关系；
（2）连接EF，AE．当S_{四边形OFEB}=3S_△OFE时，直接写m与n的大小关系及四边形OFEA的形状．

进入冬季，我市空气质量下降，多次出现雾霾天气．商场根据市民健康需要，代理销售一种防尘口罩，进货价为20元/包，经市场销售发现：销售单价为30元/包时，每周可售出200包，每涨价1元，就少售出5包．若供货厂家规定市场价不得低于30元/包，且商场每周完成不少于150包的销售任务．
（1）试确定周销售量y（包）与售价x（元/包）之间的函数关系式；
（2）试确定商场每周销售这种防尘口罩所获得的利润w（元）与售价x（元/包）之间的函数关系式，并直接写出售价x的范围；
（3）当售价x（元/包）定为多少元时，商场每周销售这种防尘口罩所获得的利润w（元）最大？最大利润是多少？

（1）解方程：4x2-8x-3=0
（2）求抛物线与x轴和y轴的交点坐标．

如图，抛物线y=ax²+bx+c的顶点为C（0，﹣），与x轴交于点A、B，连接AC、BC，得等边△ABC．T点从B点出发，以每秒1个单位的速度向点A运动，同时点S从点C出发，以每秒个单位的速度向y轴负方向运动，TS交射线BC于点D，当点T到达A点时，点S停止运动．设运动时间为t秒．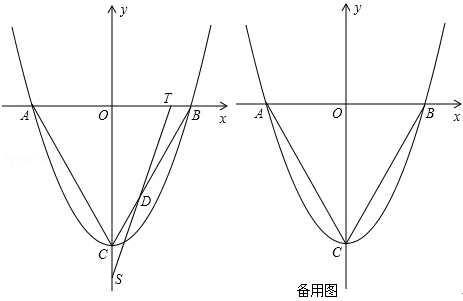

（1）求二次函数的解析式；
（2）设△TSC的面积为S，求S关于t的函数解析式；
（3）以点T为圆心，TB为半径的圆与射线BC交于点E，试说明：在点T运动的过程中，线段ED的长是一定值，并求出该定值．

已知二次函数y=x²﹣2bx+c的图象与x轴只有一个交点．
（1）请写出b、c的关系式；
（2）设直线y=7与该抛物线的交点为A、B，求AB的长；
（3）若P（a，﹣a）不在抛物线y=x²﹣2bx+c上，请求出b的取值范围．

如图，二次函数y=ax²+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．

（1）求二次函数的解析式；
（2）点P在x轴正半轴上，且PA=PC，求OP的长．