2011年初中毕业升学考试(江苏扬州卷)数学
如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC 重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
| A.3 | B.4 |
| C.5 | D.6 |
如图,正方形 的边长为4, 为正方形边上一动点,运动路线是 ,设 点经过的路程为 ,以点 、 、 为顶点的三角形的面积是 .则下列图象能大致反映 与 的函数关系的是( )





某城市在“五一”期间举行了“让城市更美好”大型书画、摄影展览活动,据统计,星期一至星期日参观的人数分别是:2030、3150、1320、1460、1090、3150、4120,则这组数据的中位数和众数分别是 .
如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,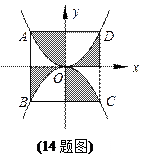
AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且经
过B、C两点的抛物线将正方形分割成几部分,则图中阴影部份的面
积是
某城市居民最低生活保障在2009年是240元,经过连续
两年的增加,到2011年提高到345.6元,则该城市两年最低生活保障的平
均年增长率是 .
如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转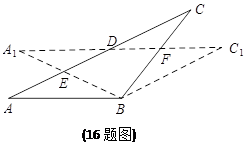 α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC
α度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC、BC
于点D、F,下列结论:①∠CDF=α,②A1E=CF,
③DF=FC,④AD =CE,⑤A1F=CE.
其中正确的是 (写出正确结论的序号).
(3)如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AF=CE,BH=DG, 求证:AG∥HE
求证:AG∥HE
某校开展了以“人生观、价值观”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
(1)该班学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度.
(2)如果该校有1500名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人.
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答)
 |
某县为鼓励失地农民自主创业,在2010年对60位自主创业的失地农民自主创业的失地农民进行奖励,共计划奖励10万元.奖励标准是:失地农民自主创业连续经营一年以上的给予1000元奖励;自主创业且解决5人以上失业人员稳定就业一年以上的,再给予2000元奖励.问:该县失地农民中自主创业连续经营一年以上的和自主创业且解决5人以上失业人员稳定就业一年以上的农民分别有多少人?
如图,一次函数的图象与反比例函数y1=" –" ( x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<–1时,一次函数值大于反比例函数的值,当x>–1时,一次函数值小于反比例函数值.
(1) 求一次函数的解析式;
(2) 设函数y2= (x>0)的图象与y1=" –" (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
 |
如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行的距离(因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个距离MN的方案,要求:
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.
 |
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧上取一点E使∠EBC = ∠DEC,延长BE依次交AC于G,交⊙O于H.
(1)求证:AC⊥BH
 (2)若∠ABC= 45°,⊙O的直径等于10,BD =8,求CE的长.
(2)若∠ABC= 45°,⊙O的直径等于10,BD =8,求CE的长.
关于反比例函数y=图象,下列说法正确的是
| A.必经过点(1,1) | B.两个分支分布在第二、四象限 |
| C.两个分支关于x轴成轴对称 | D.两个分支关于原点成中心对称 |
小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是
已知抛一枚均匀硬币正面朝上的概率为,下列说法错误的是
| A.连续抛一均匀硬币2次必有1次正面朝上 |
| B.连续抛一均匀硬币10次都可能正面朝上 |
| C.大量反复抛一均匀硬币,平均100次出现正面朝上50次 |
| D.通过抛一均匀硬币确定谁先发球的比赛规则是公平的 |
在正五边形ABCDE中,对角线AD,AC与EB分别相交于点M,N.下列结论错误的是
| A.四边形EDCN是菱形 | B.四边形MNCD是等腰梯形 |
| C.△AEM与△CBN相似 | D.△AEN与△EDM全等 |
下列调查,适合用普查方式的是( )
| A.了解一批炮弹的杀伤半径 | B.了解扬州电视台《关注》栏目的收视率 |
| C.了解长江中鱼的种类 | D.了解某班学生对“扬州精神”的知晓率 |
如图是由几个小立方块所塔成的几何的俯视图,小正方形中的数字表示该位置小立方块的个数,则该几何体的主视图是( )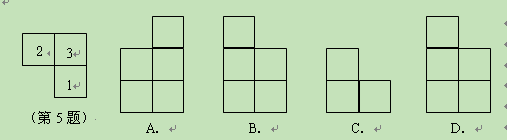
已知下列命题:①对角线互相平分的四边形是平行四边形;②等腰梯形的对角线相等;③对角线互相垂直的四边形是菱形;④内错角相等.其中假命题有( )
| A.1个 | B.2个 |
| C.3个 | D.4个 |
如图,在 中,
中,

 .将
.将 绕点
绕点 按顺时针方向旋转
按顺时针方向旋转 度后得到
度后得到 ,此时点
,此时点 在
在 边上,斜边
边上,斜边 交
交 边于点
边于点 ,则
,则 的大小和图中阴影部分的面积分别为( )
的大小和图中阴影部分的面积分别为( )
A. |
B. |
C. |
D. |

“十一五”期间,我市农民收入稳步提高,2010年农民人均纯收入达到9462元,将数据9462用科学记数法表示为______________.
数学老师布置10道选择题作业,批阅后得到如下统计表.根据表中数据可知,这45名同学答对题数组成的样本的中位数是___________题.
某公司4月份的利润为160万元,要使6月份的利润达到250万元,则平均每月增长的百分率是___________.
如图,立方体的六个面上标着连续的整数,若相对的两个面上所标之数的和相等,则这六个数的和为_____________.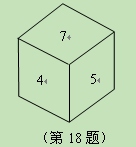
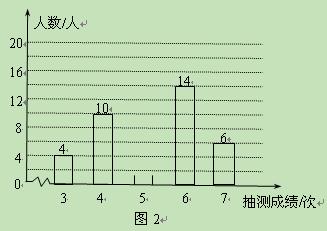
为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2两幅尚不完整的统计图.
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请你将图2中的统计图补充完整;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校350名九年级男生中估计有多少人体能达标?
扬州市体育中考现场考试内容有三项:50米跑为必测项目;另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.
(1)每位考生有__________种选择方案;
(2)用画树状图或列表的方法求小明与小刚选择同种方案的概率.(友情提醒:各种主案用 、…或①、②、③、…等符号来代表可简化解答过程)
、…或①、②、③、…等符号来代表可简化解答过程)
已知:如图,锐角 的两条高
的两条高 相交于点
相交于点 ,且
,且
(1)求证: 是等腰三角形;
是等腰三角形;
(2)判断点 是否在
是否在 的角平分线上,并说明理由.
的角平分线上,并说明理由.
古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由 两工程队先后接力完成.
两工程队先后接力完成. 工作队每天整治12米,
工作队每天整治12米, 工程队每天整治8米,共用时20天.
工程队每天整治8米,共用时20天.
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:


 甲:
甲: 乙:
乙:
根据甲、乙两名同学所列的方程组,请你分别指出未知数 表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲: 表示________________,
表示________________, 表示_______________;
表示_______________;
乙: 表示________________,
表示________________, 表示_______________.
表示_______________.
(2)求 两工程队分别整治河道多少米.(写出完整的解答过程)
两工程队分别整治河道多少米.(写出完整的解答过程)
如图是某品牌太阳能热火器的实物图和横断面示意图,已知真空集热管 与支架
与支架 所在直线相交于水箱横断面
所在直线相交于水箱横断面 的圆心
的圆心 ,支架
,支架 与水平面
与水平面 垂直,
垂直, 厘米,
厘米, ,另一根辅助支架
,另一根辅助支架 厘米,
厘米, .
.
(1)求垂直支架 的长度;(结果保留根号)
的长度;(结果保留根号)
(2)求水箱半径 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据: )
)

已知:如图,在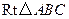 中,
中,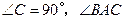 的角平分线
的角平分线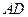 交
交 边于
边于 .
.
(1)以 边上一点
边上一点 为圆心,过
为圆心,过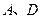 两点作
两点作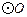 (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线 与
与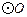 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若(1)中的 与
与 边的另一个交点为
边的另一个交点为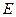 ,
, ,求线段
,求线段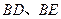 与劣弧
与劣弧 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和 )
)
如图1是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽的水匀速注入乙槽,甲、乙两个水槽中水的深度 (厘米)与注水时间
(厘米)与注水时间 (分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(1)图2中折线 表示________槽中水的深度与注水时间的关系,线段
表示________槽中水的深度与注水时间的关系,线段 表示_______槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点
表示_______槽中水的深度与注水时间之间的关系(以上两空选填“甲”或“乙”),点 的纵坐标表示的实际意义是________________________________;
的纵坐标表示的实际意义是________________________________;
(2)注水多长时间时,甲、乙两个水槽中水的深度相同?
(3)若乙槽底面积为36平方厘米(壁厚不计),求乙槽中铁块的体积;
(4)若乙槽中铁块的体积为112立方厘米,求甲槽底面积(壁厚不计).(直接写出结果)


 AC是⊙O的直径,∠P= 40°,则∠BAC= .
AC是⊙O的直径,∠P= 40°,则∠BAC= .

 的相反数是( )
的相反数是( )





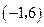 ,则下列各点中此函数图象也经过的点是( )
,则下列各点中此函数图象也经过的点是( )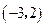
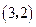
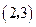
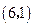
 _______________.
_______________. _______.
_______. 岛在
岛在 岛的北偏东
岛的北偏东 方向,在
方向,在 岛的北偏西
岛的北偏西 方向,则从
方向,则从 两岛的视角
两岛的视角 =__________°.
=__________°.
 的弦
的弦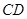 与直线径
与直线径 相交,若
相交,若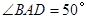 ,则
,则 =_____°.
=_____°.
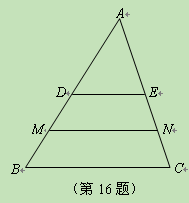
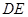 是
是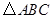 的中位数,
的中位数,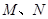 分别是
分别是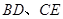 的中点,
的中点,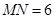 ,则
,则 _____________.
_____________.
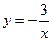 与
与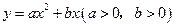 的图象交于点
的图象交于点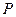 ,点
,点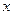 的方程
的方程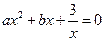 的解为_____________.
的解为_____________.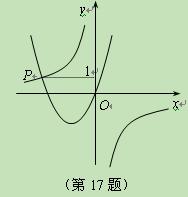
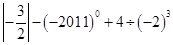 (2)
(2)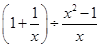
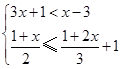 ,并写出它的所有整数解.
,并写出它的所有整数解. 中,
中, 是
是 边的中点,
边的中点, 交
交 于点
于点 .动点
.动点 从点
从点 出发沿射线
出发沿射线 以每秒
以每秒 厘米的速度运动.同时,动点
厘米的速度运动.同时,动点 从点
从点 运动,且始终保持
运动,且始终保持 设运动时间为
设运动时间为 秒(
秒( ).
). 与
与 相似吗?以图1为例说明理由;
相似吗?以图1为例说明理由; 厘米.
厘米. 的面积为
的面积为 (平方厘米),求
(平方厘米),求 三者之间的数量关系,以图1为例说明理由.
三者之间的数量关系,以图1为例说明理由.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号