廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为 ,为保护廊桥的安全,在该抛物线上距水面
,为保护廊桥的安全,在该抛物线上距水面 高为8米的点、处要安装两盏警示灯,则这两盏灯的水平距离
高为8米的点、处要安装两盏警示灯,则这两盏灯的水平距离 是 (精确到1米)
是 (精确到1米)
在函数y= (a为常数)的图象上有三点(x1,y1)、(x2,y2)、(x3,y3),且x1<x2<0<x3,则y1、y2、y3的大小关系是 。
(a为常数)的图象上有三点(x1,y1)、(x2,y2)、(x3,y3),且x1<x2<0<x3,则y1、y2、y3的大小关系是 。
.已知抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标是(5,0),(-2,0),
则方程ax2+bx+c=0(a≠0)的解是_______.
已知抛物线y=(m-1)x2,且直线y=3x+3-m经过一、二、三象限,则m的范围是 m≠1且m<3 。
如图,在抛物线 上取点B1(
上取点B1( ,
, ),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,,则A100的坐标为
),在y轴负半轴上取一个点A1,使△OB1A1为等边三角形;然后在第四象限取抛物线上的点B2,在y轴负半轴上取点A2,使△A1B2A2为等边三角形;重复以上的过程,可得△A99B100A100,,则A100的坐标为 
1) 如图,将抛物线y1=2x2向右平移2个单位,
得到抛物线y2的图象,则y2= ;
(2)P是抛物线y2对称轴上的一个动点,直线x
=t平行于y轴,分别与直线y=x、抛物线y2交
于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的
t的值,则t= .
如图,已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),则能使y1>y2成立的x的取值范围是___________。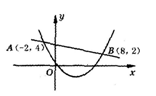
(1) 如图,将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,则y2= ;
(2)P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= .
已知(-2,y1),(-1,y2),(2,y3)是二次函数y=x2-4x+m上的点,
则y1,y2,y3从小到大用 “<”排列是 __________ .
如图,在第一象限内作射线OC,与x轴的夹角为30o,在射线OC上取一点A,过点A作AH⊥x 轴于点H.在抛物线y=x2(x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是 .