[浙江]2011-2012年浙江省衢州华外九年级上学期第二次质量检测数学卷
右图是一个几何体的三视图,则这个几何体是( ).
| A.圆锥 |
| B.圆柱 |
| C.长方体 |
| D.球体 |
已知圆锥的底面半径为6,高为8,则它的侧面积是…………………( ).
A. |
B. |
C. |
D. |
将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是( ).
| A.43° | B.47° | C.30° | D.60° |
一次函数 和反比例函数
和反比例函数 (
( ?
? ≠0)的图像如图所示,若
≠0)的图像如图所示,若 >
> ,则
,则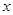 的取值范围是( ).
的取值范围是( ).
A.-2<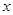 <0或 <0或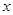 >1 >1 |
B.-2<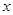 <1 <1 |
C.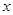 <-2或 <-2或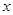 >1 >1 |
D.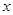 <-2或0< <-2或0<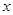 <1 <1 |
已知⊙O中,弦AB的长等于半径,P为弦AB所对的弧上一动点(不包括点A点B),则∠APB的度数为( ).
A. 30° B. 150° C. 30° 或150° D. 60°或120°
如图,⊙O的两条弦AB、CD互相垂直,垂足为点E,且⊙O的半径为2,AB与CD两弦长的平方和等于28,则OE等于( ).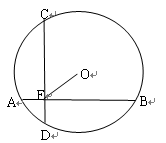
A. 1 B. 2 C. 1.5 D. 4
如图,已知△ABC的面积是 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于__________(结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于__________(结果保留根号).
(本题6分)如图,在△ABC中,BC="12cm," AB="AC," ∠BAC=120°
(1)作的外接圆(只需作出图形,并保留作图痕迹);
(2)求它的外接圆直径.
(本题6分)如图,小丽自己动手做了一顶圆锥形的圣诞帽,母线长是30cm,底面半径是10cm,她想在帽子上缠一根漂亮的丝带,从A出发绕帽子侧面一周回到 A ;
;
(1)画出该圆锥的侧面展开图,标出圆心角及半径长;
(2)丝带至少需多长?
(本题6分)如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.(1) 试判断DE与BD是否相等,并说明理由;(2) 如果BC=6,AB=5,求BE的长.
(本题10分)如图,在Rt△ABC中,∠B=90°,AB=1,BC= ,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
(1)求AE的长度;
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,
①求证:△AEG∽△FEA;
②试猜想∠EAG的大小,并说明理由.
(本题10分)问题情境


已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的一边长为x,周长为y,则y与x的函数关系式为 .
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数的图象性质.
①填写下表,画出函数的图象:
| x |
…… |
 |
 |
 |
1 |
2 |
3 |
4 |
…… |
| y |
…… |
|
|
|
|
|
|
|
…… |

|
②观察图象,试描述该函数的增减性(y随x变化发生什么变化);
③在求二次函数y=ax+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
 的相反数是( ).
的相反数是( ).


 的结果是( ).
的结果是( ).

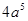
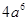
 的根是( ).
的根是( ).





 ,且顶点坐标为(-2,3)的抛物线解析式: .
,且顶点坐标为(-2,3)的抛物线解析式: .

 粤公网安备 44130202000953号
粤公网安备 44130202000953号