（本题10分）如图，在Rt△ABC中，∠B＝90°，AB＝1，BC＝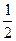
，以点C为圆心，CB为半径的弧交CA于点D；以点A为圆心，AD为半径的弧交AB于点E．
（1）求AE的长度；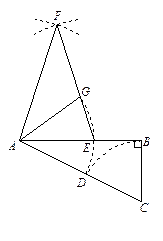
（2）分别以点A、E为圆心，AB长为半径画弧，两弧交于点F（F与C在AB两侧），连接AF、EF，设EF交弧DE所在的圆于点G，连接AG，
①求证：△AEG∽△FEA；
②试猜想∠EAG的大小，并说明理由．
（本题10分）如图，在Rt△ABC中，∠B＝90°，AB＝1，BC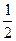＝，以点C为圆心，CB为半径的弧交CA于点D；以点A为圆心，AD为半径的弧交AB于点E．
（1）求AE的长度；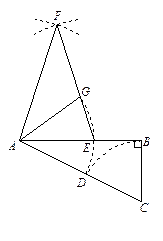
（2）分别以点A、E为圆心，AB长为半径画弧，两弧交于点F（F与C在AB两侧），连接AF、EF，设EF交弧DE所在的圆于点G，连接AG，
①求证：△AEG∽△FEA；
②试猜想∠EAG的大小，并说明理由．
粤公网安备 44130202000953号