(本题12分)如图,抛物线y=ax2+bx+c交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3)。点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行。直线y=-x+m过点C,交y轴于D点.
⑴求抛物线的函数表达式;
⑵点K为线段AB上一动点,过点K作x轴的垂线与直线CD交于点H,与抛物线交于 点G,求线段HG长度的最大值;
⑶在直线l上取点M,在抛物线上取点N,使以点A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.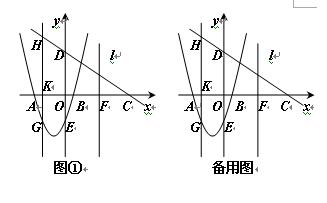
相关知识点
推荐套卷
 千克,木星的质量约为
千克,木星的质量约为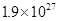 千克.问木星的质量约是地球的多少倍? (结果精确到个位)
千克.问木星的质量约是地球的多少倍? (结果精确到个位) ,其中
,其中
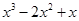
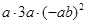
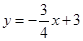 的图象与
的图象与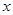 轴和
轴和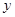 轴分别相交于A、B两点,点C在线段BA上以每秒1个单位长度的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间为
轴分别相交于A、B两点,点C在线段BA上以每秒1个单位长度的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间为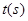 ,其中一点到达终点时,另一点也随之停止运动.
,其中一点到达终点时,另一点也随之停止运动.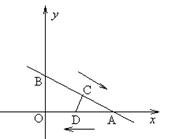
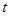 为何值时,
为何值时,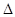 ACD的面积等于
ACD的面积等于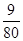 ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号