[浙江]2011年浙江省义蓬片九年级第一次阶段考试数学卷
一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些
球除颜色外,没有任何其它区别,现从这个盒子中随机摸出一个球,
摸到红球的概率为( )
A. |
B. |
C. |
D. |
如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角
顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线 (k≠0)与
(k≠0)与 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )
A.1<k<2 B.1≤k≤3
C.1≤k≤4 D.1<k<4
如图,直线 (b>0)与双曲线
(b>0)与双曲线 (x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N;有以下结论:
(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N;有以下结论:
①OA=OB
②△AOM≌△BON
③若∠AOB=45°,则S△AOB=k
④当AB= 时,ON-BN=1;
时,ON-BN=1;
其中结论正确的个数为( )
A.1 B.2 C.3 D.4
1) 如图,将抛物线y1=2x2向右平移2个单位,
得到抛物线y2的图象,则y2= ;
(2)P是抛物线y2对称轴上的一个动点,直线x
=t平行于y轴,分别与直线y=x、抛物线y2交
于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的
t的值,则t= .
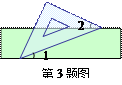
如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线)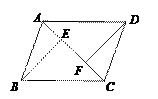
如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线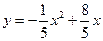 ,其中
,其中 (m)是球的飞行高度,
(m)是球的飞行高度, (m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.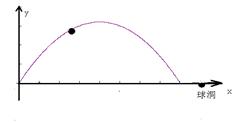
(1)请写出抛物线的开口方向、顶点坐标、对称轴.
(2)请求出球飞行的最大水平距离.
(3)若王强再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线,求出其解析式
有A、B两个黑布袋,A布袋中有两个完全相同的小球,分
别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字 ,
,
和-4.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B
布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐
标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=-X-2上的概率
如图,直线 与反比例函数
与反比例函数 的图象交于A
的图象交于A ,B
,B 两点.(1)求
两点.(1)求 、
、 的值?
的值?
(2)直接写出 时x的取值范围?
时x的取值范围?
(3)如图,等腰梯形OBCD中,BC//OD,
OB=CD,OD边在x轴上,过点C作CE
⊥OD于点E,CE和反比例函数的图象
交于点P,当梯形OBCD的面积为12时,
请判断PC和PE的大小关系,并说明
理由. 
某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为: ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式;
(2)当x取何值时,y的值最大?
(3)如果公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?


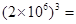 ( )
( )
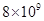
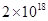
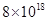
 上有两个点
上有两个点 ,
, ,其中
,其中 ,
, 与
与 的大小关系是( )
的大小关系是( ) B.
B. C.
C. D.以上都有可能
D.以上都有可能 向左平移1个单位,然后向下平移3个单位,则平移后抛物线的解析式为( )
向左平移1个单位,然后向下平移3个单位,则平移后抛物线的解析式为( )



 与
与 在第一象限内的图象如图所示,作
在第一象限内的图象如图所示,作
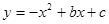 的部分图象如上图所示,若
的部分图象如上图所示,若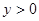 ,则
,则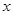 的取值范围是( )
的取值范围是( )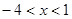
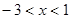
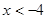 或
或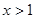
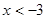 或
或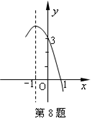
 有意义,则a的取值范围为____________.
有意义,则a的取值范围为____________.
 的图象
的图象 在第二
在第二 、四象限,则m的取值范围为 .
、四象限,则m的取值范围为 . 的顶点
的顶点 在
在 轴的正半轴上,如图将正方形
轴的正半轴上,如图将正方形 顺时针旋转
顺时针旋转 得正方形
得正方形 ,使点
,使点 恰好落在函数
恰好落在函数 的图像上,则
的图像上,则 的值为 。
的值为 。


 经过点P(
经过点P( ,
, ),点P关
),点P关 轴的对称点P′在反比例函数
轴的对称点P′在反比例函数 (
( )的图象上.
)的图象上. (1)求
(1)求 ,直线y=
,直线y= 经过点C,交y轴于点G,且∠AGO=30°。
经过点C,交y轴于点G,且∠AGO=30°。 平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存
平移,平移后的抛物线交y轴于点F,顶点为点E。平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存 在,请求出此时抛物线的解析式;若不存在,请说明理由。
在,请求出此时抛物线的解析式;若不存在,请说明理由。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号