已知下列函数 ① ②
② ③
③ ,其中,图象通过平移可以得到函数
,其中,图象通过平移可以得到函数 的图像的有 ▲ (填写所有正确选项的序号)
的图像的有 ▲ (填写所有正确选项的序号)
从 、0、1、2这四个数中任取一个数作为点
、0、1、2这四个数中任取一个数作为点 的横坐标,再从剩下的三个数中任取一个作为点
的横坐标,再从剩下的三个数中任取一个作为点 的纵坐标,则点
的纵坐标,则点 落在抛物线
落在抛物线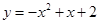 与直线
与直线 所围成的区域内(不含边界)的概率为 。
所围成的区域内(不含边界)的概率为 。
已知⊙P的半径为1,圆心P在抛物线y=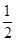 x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为 .
x2-1上运动,当⊙P与x轴相切时,圆心P的坐标为 .
对于二次函数 ,有下列说法:①它的图象与
,有下列说法:①它的图象与 轴有两个公共点;②如果当
轴有两个公共点;②如果当 ≤1时
≤1时 随
随 的增大而减小,则
的增大而减小,则 ;③如果将它的图象向左平移3个单位后过原点,则
;③如果将它的图象向左平移3个单位后过原点,则 ;④如果当
;④如果当 时的函数值与
时的函数值与 时的函数值相等,则当
时的函数值相等,则当 时的函数值为
时的函数值为 .其中正确的说法是 .(把你认为正确说法的序号都填上)
.其中正确的说法是 .(把你认为正确说法的序号都填上)
如图,在第一象限内作射线OC,与x轴的夹角为30o,在射线OC上取一点A,过点A作AH⊥x轴于点H。在抛物线y=x2 (x>0)上取点P,在y轴上取点Q,使得以P,O,Q为顶点的三角形与△AOH全等,则符合条件的点A的坐标是 .
九年级数学课本上,用“描点法”画二次函数 的图象时,列了如下表格:
的图象时,列了如下表格:
 |
… |
 |
 |
0 |
1 |
2 |
… |
 |
… |
 |
 |
 |
 |
 |
… |
根据表格上的信息回答问题:该二次函数 图象的对称轴为直线
图象的对称轴为直线 ,当
,当 时,函数值
时,函数值 。
。
如图为二次函数 的图象,
的图象,
给出五种说法:①ab<0;
②方程 的根为
的根为 =-1,
=-1, =3;
=3;
③a+b+c>0;④当x>1时,y随x的增大而增大;
⑤当y>0时,-1<x<3.
其中,正确的说法有
(把你认为正确的说法的序号都填上).
在直角坐标系中,有以A(-1,-1),B(1,-1),C(1,1),D(-1,1)为顶点的正方形,设它在折线 上侧部分的面积为S.当
上侧部分的面积为S.当 时,S= ▲ ;当
时,S= ▲ ;当 为任意实数时,面积S的最大值为 ▲ .
为任意实数时,面积S的最大值为 ▲ .
当-2<x<2时,下列函数中,y随x增大而增大的是_________(只填序号).
①y=2x ②y=2-x ③y=-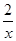 ④y=x2+6x+8
④y=x2+6x+8
有七张正面分别标有数字 ,
, ,
, ,0,l,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为
,0,l,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为 ,则使关于
,则使关于 的一元二次方程
的一元二次方程 有两个不相等的实数根,且以
有两个不相等的实数根,且以 为自变量的二次函数
为自变量的二次函数 的图象不经过点(1,O)的概率是________.
的图象不经过点(1,O)的概率是________.
已知抛物线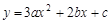 ,
,
(1)若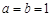 ,
,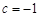 ,求该抛物线与
,求该抛物线与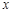 轴公共点的坐标;
轴公共点的坐标;
(2)若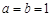 ,且当
,且当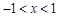 时,抛物线与
时,抛物线与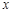 轴有且只有一个公共点,求
轴有且只有一个公共点,求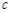 的取值范围;
的取值范围;
(3)若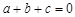 ,且
,且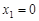 时,对应的
时,对应的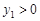 ;
;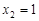 时,对应的
时,对应的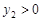 ,试判断当
,试判断当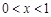 时,抛物线与
时,抛物线与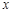 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.
如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2),则抛物线的对称轴是 ;若y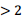 ,则自变量x的取值范围是 .
,则自变量x的取值范围是 . 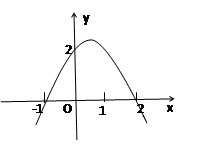
如图,点A,B,M的坐标分别为(1, 4)、(4, 4)和(-1,0),抛物线 的顶点在线段AB(包括线段端点)上,与x轴交于C、D两点,点C在线段OM上(包括线段端点),则点D的横坐标m的取值范围是 ▲ .
的顶点在线段AB(包括线段端点)上,与x轴交于C、D两点,点C在线段OM上(包括线段端点),则点D的横坐标m的取值范围是 ▲ .