如图,二次函数 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与 轴相交于负半轴.(以下有(1)、(2)两问,每个考生只须选答一问,若两问都答,则只以第(2)问计分)
轴相交于负半轴.(以下有(1)、(2)两问,每个考生只须选答一问,若两问都答,则只以第(2)问计分)
第(1)问:给出四个结论:①  ;②
;②  ;③
;③  ;④
;④  .
.
其中正确结论的序号是 .
第(2)问:给出四个结论:①  ;②
;②  ;③
;③  ;④
;④ .其中正确结论的序号是 .
.其中正确结论的序号是 .
如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需 秒.
二次函数 的图像与
的图像与 轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有 个(提示:必要时可利用下面的备用图画出图像来分析).
轴围成的封闭区域内(包括边界),横、纵坐标都是整数的点有 个(提示:必要时可利用下面的备用图画出图像来分析).
如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .
函数图象y=ax2+(a-3)x+1与x轴只有一个交点则a的值为 .
如图,已知矩形ABCD中AB:BC=3:1,点A、B在x轴上,直线y="mx+n" (0<m<n< ),过点A、C交y轴于点E,S△AOE=S矩形ABCD,抛物线y=ax2+bx+c过点A、B,且顶点G在直线y=mx+n上,抛物线与y轴交于点F.
),过点A、C交y轴于点E,S△AOE=S矩形ABCD,抛物线y=ax2+bx+c过点A、B,且顶点G在直线y=mx+n上,抛物线与y轴交于点F.
(1)点A的坐标为_____________;B的坐标______________(用n表示);
(2)abc= .
如图,一次函数y=-2x的图象与二次函数y=-x2+3x图象的对称轴交于点B.
(1)写出点B的坐标 ;
(2)已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于C、D两点. 若以CD为直角边的△PCD与△OCD相似,则点P的坐标为 .
抛物线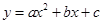 上部分点的横坐标
上部分点的横坐标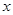 ,纵坐标
,纵坐标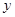 的对应值如下表:
的对应值如下表:
| x |
… |
-2 |
-1 |
0 |
1 |
2 |
… |
| y |
… |
0 |
4 |
6 |
6 |
4 |
… |
从上表可知,下列说法中正确的是 .(填写序号)
①抛物线与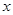 轴的一个交点为(3,0); ②函数
轴的一个交点为(3,0); ②函数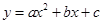 的最大值为6;
的最大值为6;
③抛物线的对称轴是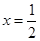 ; ④在对称轴左侧,
; ④在对称轴左侧,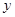 随
随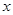 增大而增大.
增大而增大.
正方形A1B1C1C0,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C0,C1,C2,C3,…分别在抛物线y=ax2(a>0)和x轴上,已知B1(3,1),B2( ,
, ),则a= ,Bn的坐标为 . (根据2009年山东省中考题改编)
),则a= ,Bn的坐标为 . (根据2009年山东省中考题改编)
已知抛物线 与直线y=kx都经过原点和点E
与直线y=kx都经过原点和点E .
.
(1) k= ;
(2)如图,点P是直线y=kx(x>0)上的一个动点,过点P作 轴的
轴的
垂线,垂足是点C,交抛物线于点B,过点B作 轴的平行线
轴的平行线
交直线y=kx于点D,连结OB;若以B、P、D为顶点的三角形
与△OBC相似,则点P的坐标是 .
如图,一次函数y=-2x的图象与二次函数y=-x2+3x图象的对称轴交于点B.
(1)写出点B的坐标 ;
(2)已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于C、D两点. 若以CD为直角边的△PCD与△OCD相似,则点P的坐标为 .
给出下列命题:
命题1.点(1,1)是双曲线 与抛物线
与抛物线 的一个交点.
的一个交点.
命题2.点(1,2)是双曲线 与抛物线
与抛物线 的一个交 点.
的一个交 点.
命题3.点(1,3)是双曲线 与抛物线
与抛物线 的一个交点.
的一个交点.
……