[山东]2012届山东省聊城市高唐县九年级上学期期末考试数学试卷
四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判定这个四边形是平行四边形的条件有
A.1组 B.2组 C.3组 D.4组
已知x=1是方程x2+bx-2=0的一个根,则方程的另一个根是
| A.1 | B.2 | C.-1 | D.-2 |
已知一个四边形的对角线互相垂直,那么顺次连接这个四边形的四边中点所得的四边形是
| A.矩形 | B.菱形 | C.等腰梯形 | D.正方形 |
正方形具有而菱形不一定具有的性质是
| A.四条边相等 | B.对角线互相垂直平分 |
| C.对角线平分一组对角 | D.对角线相等 |
已知弧CD是⊙O的一条弧,点A是弧CD的中点,连接AC,CD.则
A.CD=2AC B.CD>2AC C.CD<2AC D.不能确定.
某商品原售价289元,经过连续两次降价后售价为256元,设平均每次降价的百分率为x,则下面所列方程中正确的是
A. |
B. |
| C.289(1-2x)=256 | D.256(1-2x)=289 |
下列二次函数中,图象以直线x = 2为对称轴,且经过点(0,1)的是
| A.y = (x − 2)2 + 1 | B.y = (x + 2)2 + 1 |
| C.y = (x − 2)2 − 3 | D.y = (x + 2)2 − 3 |
下面图形都是由同样大小的平行四边形按一定的规律组成,其中,第①个图形一共有1个平行四边形,第②个图形一共有5个平行四边形,第③个图形一共有11个平行四边形,……,则第⑥个图形中平行四边形的个数为
| A.55 | B.41 | C.42 | D.29 |
在直角三角形中,若两条直角边长分别为6cm和8cm,则三角形的内切圆半径与外接圆半径之比为 .
已知⊙O1与⊙O2的半径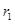 、
、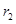 分别是方程
分别是方程 的两实根,若⊙O1与⊙O2的圆心距
的两实根,若⊙O1与⊙O2的圆心距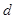 =5.则⊙O1与⊙O2的位置关系是___ _
=5.则⊙O1与⊙O2的位置关系是___ _
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB = 3 cm,BC = 5 cm,则重叠部分△DEF的面积是 cm2.
如图,在由边长为 的小正方形组成的方格纸中,有两个全等的三角形,即△A1B1C1和△A2B2C2.
的小正方形组成的方格纸中,有两个全等的三角形,即△A1B1C1和△A2B2C2.
(1)请你指出在方格纸内如何运用平移、旋转变换,将△A1B1C1重合到△A2B2C2上;
(2)在方格纸中将△A1B1C1经过怎样的变换后可以与△A2B2C2成中心对称图形?画出变换后的三角形并标出对称中心.
如图:两个同心圆的半径所截得的弧长AB=6 cm,CD=10
cm,CD=10 cm,且AC=12cm。(1)求两圆的半径长。(2)阴影部分的面积是多少?
cm,且AC=12cm。(1)求两圆的半径长。(2)阴影部分的面积是多少? 
商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:
(1)商场日销售量增加 件,每件商品盈利 元(用含x的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由. 
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系,求:(1)以这一部分抛物线为图象的函数解析式,并写出x的取值范围;(2)有一辆宽2.8米,高1米的农用货车(货物最高处与地面AB的距离)能否通过此隧道?
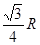
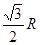
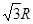
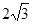 R
R




 的图像如图所示,反比列函数
的图像如图所示,反比列函数 与正比列函数
与正比列函数 在同一坐标系内的大致图像是
在同一坐标系内的大致图像是
 (用配方法)
(用配方法) (因式分解)
(因式分解) 是平行四边形
是平行四边形 的对角线
的对角线 上的点,
上的点, ,请你猜想:线段
,请你猜想:线段 与线段
与线段 有怎样的关系?并对你的猜想加以证明。
有怎样的关系?并对你的猜想加以证明。
 ,∠CAC ¢ =
,∠CAC ¢ = ,试探索
,试探索
 粤公网安备 44130202000953号
粤公网安备 44130202000953号