如图，Rt△AB ¢C ¢是由Rt△ABC绕点A顺时针旋转得到的，连结CC ¢交斜边于点E，CC ¢的延长线交BB ¢于点F．
（1）证明：△ACE∽△FBE；
（2）设∠ABC=
，∠CAC ¢ =
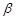，试探索、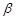满足什么关系时，△ACE与△FBE是全等三角形，并说明理由．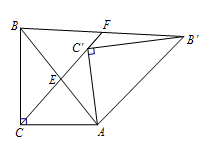
的一个实数根，求该三角形的面积。 
，其中
．推荐套卷
如图，Rt△AB ¢C ¢是由Rt△ABC绕点A顺时针旋转得到的，连结CC ¢交斜边于点E，CC ¢的延长线交BB ¢于点F．
（1）证明：△ACE∽△FBE；
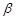（2）设∠ABC=，∠CAC ¢ =，试探索、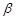满足什么关系时，△ACE与△FBE是全等三角形，并说明理由．
粤公网安备 44130202000953号