2011学年度上海市青浦区九年级数学学业模拟考试1
已知二次函数y=ax2+bx+c的图象的顶点坐标为 (0, ),且 ac=
),且 ac= .
.
(1)若该函数的图象经过点(-1,-1).
①求使y<0成立的x的取值范围.
②若圆心在该函数的图象上的圆与x轴、y轴都相切,求圆心的坐标.
(2)经过A(0,p)的直线与该函数的图象相交于M,N两点,过M,N作x轴的垂线,垂足分别为M1,N1,设△MAM1,△A M1N1,△ANN1的面积分别为s1,s2,s3,是否存在m,使得对任意实数p≠0都有s22=ms1s3成立,若存在,求出m的值,若不存在,请说明理由.
M1N1,△ANN1的面积分别为s1,s2,s3,是否存在m,使得对任意实数p≠0都有s22=ms1s3成立,若存在,求出m的值,若不存在,请说明理由.
(11·贵港)下列说法正确的是
| A.为了了解全国中学生的心理健康情况,应采用全面调查的方式 |
| B.一组数据5,6,7,6,6,8,10的众数和中位数都是6 |
| C.一个游戏的中奖概率是0.1,则做10次这样的游戏一定会中奖 |
| D.若甲组数据的方差S甲2=0.05,乙组数据的方差S乙2=0.1,则乙组数据比甲组数据稳定 |
(11·贵港)若关于x的一元二次方程x2-mx-2=0的一个根为-1,则另一个根为
| A.1 | B.-1 | C.2 | D.-2 |
(11·贵港)如图所示,在△ABC中,∠C=90°,AD是BC边上的中线,BD=4,
AD=2 ,则tan∠CAD的值是
,则tan∠CAD的值是
| A.2 | B. |
C. |
D. |

(11·贵港)如图所示,在矩形ABCD中,AB= ,BC=2,对角线AC、BD
,BC=2,对角线AC、BD
相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是
A. B.
B. C.1 D.1.5
C.1 D.1.5
(11·贵港)如图所示,在梯形ABCD中,AB∥CD,E是BC的中点,EF⊥AD
于点F,AD=4,EF=5,则梯形ABCD的面积是
| A.40 | B.30 | C.20 | D.10 |

(11·贵港)如图所示,正方形OEFG和正方形ABCD是位似图形,点F的坐标
为(-1,1),点C的坐标为(-4,2),则这两个正方形位似中心的坐标是 _ ▲ .
(11·贵港)从2,3,4,5这四个数字中,任意抽取两个不同数字组成一个两位
数,则这个两位数能被3整除的概率是_ ▲ .
(11·贵港)如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、
AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是
_ ▲ .
(11·贵港)如图所示,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四
边形ABCD,若AD=6cm,∠ABC=60°,则四边形ABCD的面积等于_ ▲ cm2.
(11·贵港)如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中
点,⊙O与AC、BC分别相切于点D、E,点F是⊙O与AB的一个交点,连接DF并延长
交CB的延长线于点G,则BG的长是_ ▲ .
(11·贵港)若记y=f(x)= ,其中f(1)表示当x=1时y的值,即f(1)=
,其中f(1)表示当x=1时y的值,即f(1)=
= ;f(
;f( )表示当x=
)表示当x= 时y的值,即f(
时y的值,即f( )=
)= =
= ;…;则f(1)+f(2)+f(
;…;则f(1)+f(2)+f( )+f(3)
)+f(3)
+f( )+…+f(2011)+f(
)+…+f(2011)+f( )=_ ▲ .
)=_ ▲ .
(11·贵港)(本题满分11分,第(1)题5分,第(2)题6分)
(1)(11·贵港)计算:(-1)2011+ -2sin60º+|-1|;
-2sin60º+|-1|;

(11·贵港)如图所示,反比例函数y= 的图象与一次函数y
的图象与一次函数y
=kx-3的图象在第一象限内相交于点A (4,m).
(1)求m的值及一次函数的解析式;
(2)若直线x=2与反比例和一次函数的图象分别交于点B、C,求线段BC的长.
(11·贵港)
按要求用尺规作图(只保留作图痕迹,不必写出作法)
(1)在图(1)中作出∠ABC的平分线;(2)在图(2)中作出△DEF的外接圆O.
(11·贵港)
“校园手机”现象越来越受到社会的关注.为了了解学生和家长对中学生带手机的态度,某记者随机调查了城区若干名学生和家长的看法,调查结果分为:赞成、无所谓、反对,并将调查结果绘制成如下不完整的统计表和统计图:
根据以上图表信息,解答下列问题:
( 1)统计表中的A=_ ▲ ;
1)统计表中的A=_ ▲ ;
(2)统计图中表示 家长“赞成”的圆心角的度数为_ ▲ 度;
家长“赞成”的圆心角的度数为_ ▲ 度;
(3)从这次接受调查的学生中,随机抽查一个,恰好是持“反对”态度的学生的概率是多少?
(11·贵港)
如图所示,在梯形ABCD中,AD∥BC,AB=AD,∠BAD的平分线AE交BC于点E,连接DE.
(1)求证:四边形ABED是菱形;
(2)若∠ABC=60°, CE=2BE,试判断△CDE的形状,并说明理由.
CE=2BE,试判断△CDE的形状,并说明理由.
已知反比例函数 ,下列结论不正确的是 ……………………( )
,下列结论不正确的是 ……………………( )
| A.图象必经过点(-1,3); | B. 随 随 的增大而增大; 的增大而增大; |
| C.图象位于第二、四象限内; | D.若 ,则 ,则 . . |
在平面直角坐标系内,把点 (-3,1)向右平移一个单位,则得到的对应点
(-3,1)向右平移一个单位,则得到的对应点 的坐标是( )
的坐标是( )
| A.(-3,2); | B.(-3,0); | C.(-4,1); | D.(-2,1). |
在 中,点
中,点 、
、 、
、 分别在
分别在 、
、 、
、 上,且
上,且 ,
, ,则下列三种说法:
,则下列三种说法:
①如果 ,那么四边形
,那么四边形 是矩形;
是矩形;
②如果 平分
平分 ,那么四边形
,那么四边形 是菱形;
是菱形;
③如果 且
且 ,那么四边形
,那么四边形 是菱形.
是菱形.
其中正确的有 ………………………………………( )
| A.3个; | B.2个; | C.1个; | D.0个. |

在 中,
中, ,且两边长分别为4
,且两边长分别为4 和5
和5 ,若以点
,若以点 为圆心,3
为圆心,3 为半径作⊙
为半径作⊙ ,以点
,以点 为圆心,2
为圆心,2 为半径作⊙
为半径作⊙ ,则⊙
,则⊙ 和⊙
和⊙ 位置关系是………( )
位置关系是………( )
| A.只有外切一种情况; | B.只有外离一种情况; |
| C.有相交或外切两种情况; | D.有外离或外切两种情况. |
为了解居民节约用水的情况,小丽对某个单元的住户用水量进行调查,右表是某
个单元的住户3月份用水量的调查结果。根据表中所提供的信息,这12户居民月用水量的
众数是 .
如图,E、F是矩形ABCD对角线AC上的两点,试添加一个条件:___________,
使得△ADF≌△CBE.
如图,光源P在横杆AB的上方,AB在灯光下的影子为CD,AB∥CD,已知AB
=2m,CD=6m,点P到CD的距离是2.7m,那么AB与CD间的距离是________m.
如图,已知边长为3的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且 ,则CE的长是 .
,则CE的长是 .
“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的 看法,统计整理并制作了如下的统计图:
看法,统计整理并制作了如下的统计图: 
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少?
如图, 、
、 两地被一大山阻隔,汽车从
两地被一大山阻隔,汽车从 地到
地到 地须经过
地须经过 地中转.为了促进
地中转.为了促进 、
、 两地的经济发展,现计划开通隧道,使汽车可以直接从
两地的经济发展,现计划开通隧道,使汽车可以直接从 地到
地到 地.已知
地.已知 ,
, ,
, 千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从
千米.若汽车的平均速度为45千米/时,则隧道开通后,汽车直接从 地到
地到 地需要多长时间?(参考数据:
地需要多长时间?(参考数据: )
)
如图,在直角梯形ABCD中,AD∥BC,∠A=90o,BD⊥DC,BC=10cm,CD=6cm.在线段 、
、 上有动点
上有动点 、
、 ,点
,点 以每秒
以每秒 的速度,在线段
的速度,在线段 上从点B向点C匀速运动;同时点
上从点B向点C匀速运动;同时点 以每秒
以每秒 的速度,在线段
的速度,在线段 上从点C向点D匀速运动.当点
上从点C向点D匀速运动.当点 到达点C时,点
到达点C时,点 同时停止运动.设点
同时停止运动.设点 运动的时间为t(秒).
运动的时间为t(秒).
(1)求AD的长;
(2)设四边形BFED的面积为 ,求y 关于t的函数关系式,并写出函数定义域;
,求y 关于t的函数关系式,并写出函数定义域;
(3)点 、
、 在运动过程中,如
在运动过程中,如 与
与 相似,求线段
相似,求线段 的长.
的长.






 经过点(1,-2),则k的值是_ ▲ .
经过点(1,-2),则k的值是_ ▲ .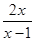 =1的解是x=_ ▲ .
=1的解是x=_ ▲ . 的结果是……………………………………………………( )
的结果是……………………………………………………( ) ;
; ;
; ;
; .
.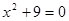 ;
; ;
;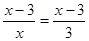 ;
;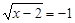 .
. .
. ,
, ,则
,则 .
. .
. 的解是 .
的解是 . 的定义域是 .
的定义域是 . 为对称轴,且在对称轴右侧部分是下降的抛物线的表
为对称轴,且在对称轴右侧部分是下降的抛物线的表 ,则这个正多边形的边数是________.
,则这个正多边形的边数是________. =
= ,
, =
= ,那么
,那么 =________.
=________.
 .
. 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
 是⊙
是⊙ 的弦,点D是弧AB的中点,过B作A
的弦,点D是弧AB的中点,过B作A B的垂线交AD的延长线于C.求证:AD=DC.
B的垂线交AD的延长线于C.求证:AD=DC.
 为原点,
为原点, 抛物线
抛物线 经过点
经过点 (
( ,
, ),且顶点
),且顶点 (
( ,
, 上.
上. 上有一点
上有一点 ,满足
,满足 ,在
,在 轴上有一点
轴上有一点 (
( ,
, ),联结
),联结 ,且直线
,且直线 轴交于点
轴交于点 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号