已知二次函数y=ax2+bx+c的图象的顶点坐标为 (0，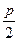
)，且 ac=
．
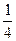（1）若该函数的图象经过点（-1，-1）．
①求使y＜0成立的x的取值范围．
②若圆心在该函数的图象上的圆与x轴、y轴都相切，求圆心的坐标．
（2）经过A（0，p）的直线与该函数的图象相交于M，N两点，过M，N作x轴的垂线，垂足分别为M1，N1，设△MAM1，△A
M1N1，△ANN1的面积分别为s1，s2，s3，是否存在m，使得对任意实数p≠0都有s22=ms1s3成立，若存在，求出m的值，若不存在，请说明理由．
相关试题
在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，表是活动进行中的一组统计数据：
| 摸球的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
| 摸到白球的次数m |
68 |
109 |
136 |
345 |
368 |
701 |
| 摸到乒乓球的频率 |
0.68 |
0.73 |
0.68 |
0.69 |
0.70 |
0.70 |
（1）请估计：当n很大时，摸到白球的频率将会接近________；
（2）假如你去摸一次，你摸到白球的概率是_______，摸到黑球的概率是_______；
（3）试估算口袋中黑、白两种颜色的球各有多少只？
（2）
如图，在平面直角坐标系中，点A、B的坐标分别为（-5，0）和（5，0），以AB为直径在x轴的上方作半圆O，点C是该半圆上第一象限内的一个动点，连结AC、BC，并延长BC至点D，使BC=CD，过点D作x轴的垂线，分别交x轴、线段AC于点E、F，E为垂足，连结OF．
（1）当∠CAB=30°时，求弧BC的长；
（2）当AE=6时，求弦BC的长；
（3）在点C运动的过程中，是否存在以点O、E、F为顶点的三角形与△DEB相似？若存在，请求出此时E点的坐标；若不存在，请说明理由．
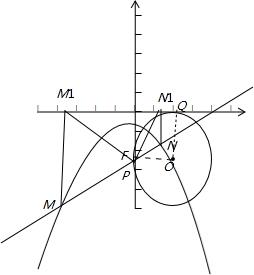
，求证：CE＋CD＝BD.相关知识点
推荐套卷
粤公网安备 44130202000953号