如图,在直角坐标平面内,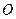 为原点,
为原点, 抛物线
抛物线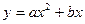 经过点
经过点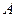 (
(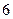 ,
,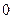 ),且顶点
),且顶点 (
( ,
,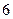 )在直线
)在直线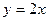 上.
上.
(1)求 的值和抛物线
的值和抛物线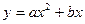 的解析式;
的解析式;
(2)如在线段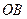 上有一点
上有一点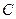 ,满足
,满足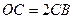 ,在
,在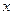 轴上有一点
轴上有一点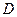 (
( ,
,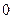 ),联结
),联结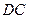 ,且直线
,且直线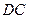 与
与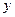 轴交于点
轴交于点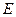 .
.
①求直线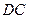 的解析式;
的解析式;
②如点M是直线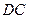 上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请求出点N的坐标.(直接写出结果,不需要过程.)
上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请求出点N的坐标.(直接写出结果,不需要过程.)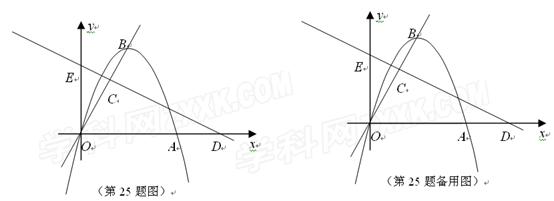
相关知识点
推荐套卷
如图,在直角坐标平面内, 为原点,
为原点, 抛物线
抛物线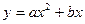 经过点
经过点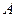 (
(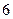 ,
,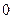 ),且顶点
),且顶点 (
( ,
,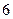 )在直线
)在直线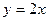 上.
上.
(1)求 的值和抛物线
的值和抛物线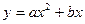 的解析式;
的解析式;
(2)如在线段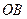 上有一点
上有一点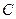 ,满足
,满足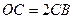 ,在
,在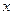 轴上有一点
轴上有一点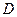 (
( ,
,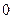 ),联结
),联结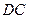 ,且直线
,且直线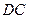 与
与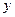 轴交于点
轴交于点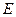 .
.
①求直线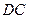 的解析式;
的解析式;
②如点M是直线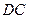 上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请求出点N的坐标.(直接写出结果,不需要过程.)
上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请求出点N的坐标.(直接写出结果,不需要过程.)