如图,已知AB是⊙O的直径,点C、D在⊙O上,过D点作PF∥AC交⊙O于F,交AB于点E,∠BPF=∠ADC.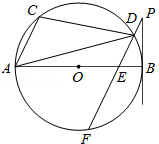
(1)求证:BP是⊙O的切线;
(2)求证:AE•EB=DE•EF;
(3)当⊙O的半径为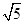 ,AC=2,BE=1时,求BP的长.
,AC=2,BE=1时,求BP的长.
相关知识点
推荐套卷
如图,已知AB是⊙O的直径,点C、D在⊙O上,过D点作PF∥AC交⊙O于F,交AB于点E,∠BPF=∠ADC.
(1)求证:BP是⊙O的切线;
(2)求证:AE•EB=DE•EF;
(3)当⊙O的半径为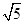 ,AC=2,BE=1时,求BP的长.
,AC=2,BE=1时,求BP的长.