如图,在矩形ABCD中,AB=5,BC=4,E、F分别是AB、AD的中点.动点从点B出发,沿B→C→D→F方向运动至点处停止.设点运动的路程为,的面积为,当取到最大值时,点应运动到
A.的中点处 B.点处
C.的中点处 D.点处
如图,在平面直角坐标系中,点A的坐标为(1, ) ,点B在x轴的负半轴上,
) ,点B在x轴的负半轴上,
∠ABO=30°.
(1)求过点A、O、B的抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点C,使AC+OC的值最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)在(1)中 轴下方的抛物线上是否存在一点P,过点P作
轴下方的抛物线上是否存在一点P,过点P作 轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
轴的垂线,交直线AB于点D,线段OD把△AOB分成两个三角形.使其中一个三角形面积与四边形BPOD面积比为2:3 ?若存在,求出点P的坐标;若不存在,请说明理由.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
①a>0.
②该函数的图象关于直线 对称.
对称.
③当 时,函数y的值都等于0.
时,函数y的值都等于0.
其中正确结论的个数是
| A.3 | B.2 | C.1 | D.0 |
如图,抛物线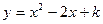 与x轴交于A、B两点,与y轴交于点C(0,-3)[图14(2)、图14(3)为解答备用图.
与x轴交于A、B两点,与y轴交于点C(0,-3)[图14(2)、图14(3)为解答备用图.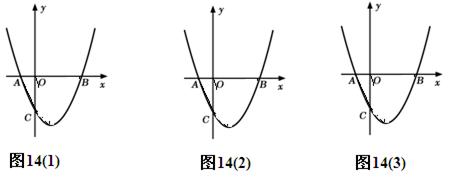
(1)k=_______,点A的坐标为___________,点C的坐标为_____________.
(2)设抛物线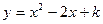 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是
| A.y=(x-1)2+2 | B. |
C. |
D. |
. 已知二次函数 的图象如图所示,有下列四个结论:
的图象如图所示,有下列四个结论:
①b<0;②c>0;③b2-4ac>0;④a-b+c<0,其中正确的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,抛物线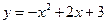 与
与 轴相交于
轴相交于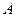 、
、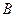 两点(点
两点(点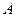 在点
在点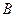 的左侧),与
的左侧),与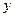 轴相交于点
轴相交于点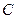 ,顶点为
,顶点为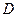 .
.
(1)直接写出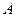 、
、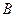 、
、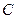 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)连接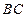 ,与抛物线的对
,与抛物线的对 称轴交于点
称轴交于点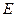 ,点
,点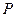 为线段
为线段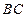 上的一个动点,过点
上的一个动点,过点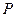 作
作 交抛物线于点
交抛物线于点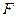 ,设点
,设点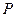 的横坐标为
的横坐标为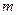 ;
;
①用含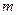 的代数式表示线段
的代数式表示线段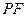 的长,并求出当
的长,并求出当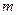 为何值时,四边形
为何值时,四边形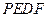 为平行四边形?
为平行四边形?
②设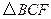 的面积为
的面积为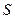 ,求
,求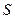 与
与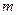 的函数关系式
的函数关系式
已知抛物线C: ,将抛物线C平移得到抛物线C,若两条抛物线C、C关于直线x=1对称,则下列平移方法中,正确的是( )
,将抛物线C平移得到抛物线C,若两条抛物线C、C关于直线x=1对称,则下列平移方法中,正确的是( )
(A)将抛物线C向右平移 个单位 (B)将抛物线C向右平移3个单位
个单位 (B)将抛物线C向右平移3个单位
(C)将抛物线C向右平移5个单位 (D)将抛物线C向右平移6个单位
已知:如图所示,关于 的抛物线
的抛物线 与
与 轴交于点
轴交于点 、点
、点 ,与
,与 轴交于点
轴交于点 .
.
(1)求出此抛物线的解析式,并写出顶点坐标;
(2)在抛物线上有一点 ,使四边形
,使四边形 为等腰梯形,写出点
为等腰梯形,写出点 的坐标,并求出直线
的坐标,并求出直线 的解析式;
的解析式;
(3)在(2)中的直线 交抛物线的对称轴于点
交抛物线的对称轴于点 ,抛物线上有一动点
,抛物线上有一动点 ,
, 轴上有一动点
轴上有一动点 .是否存在以
.是否存在以 为顶点的平行四边形?如果存在,请直接写出点
为顶点的平行四边形?如果存在,请直接写出点 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量 达到100辆.
达到100辆.
(1)若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2009年底家庭轿车将达到多少 辆?
辆?
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两 种车位各多少个?试写出所有可能的方案
种车位各多少个?试写出所有可能的方案
如图二次函数y=ax2+bx+c的图象经过A 、B、C三点。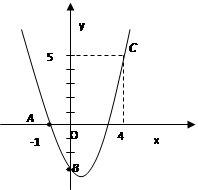
(1)观察图象,写出A 、B、C三点的坐标,并求出抛物线解析式;
(2)求此抛物线的顶点坐标和对称轴;
(3)观察图象,当x取何值时,y<0?y=0?y>0?