北京市东城区初三第二学期综合练习(一)数学试题
将直径为60cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的底面半径为 ( ▲ )
| A.10cm | B.20cm | C.30cm | D.60cm |
在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为 ( ▲ )
| A.9.5 | B.10.5 | C.11 | D.15.5 |
如图,正方形ABCD中,E是BC边上一点,以E为圆心、EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则S四边形ADCE∶S正方形ABCD的值为 ( ▲ )
A. B. C. D.
小聪在一个正方体盒子的每个面上都写有一个字,分别为“遨”、 “游”、“数”、“学”、“世”、“界”,其平面展开图如图所示,那么在这个正方体盒子中,和“数”相对的面上所写的字是 .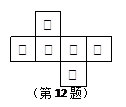
如图,D是反比例函数 的图像上一点,过D作DE⊥
的图像上一点,过D作DE⊥ 轴于E,DC⊥
轴于E,DC⊥ 轴于C,一次函数
轴于C,一次函数 与
与 的图象都经过点C,与
的图象都经过点C,与 轴分别交于A、B两点,四边形DCAE的面积为4,则
轴分别交于A、B两点,四边形DCAE的面积为4,则 的值为 .
的值为 .
如图,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此,可依次得到点E4、E5、…、En,分别记△BCE1、△BCE2、△BCE3···△BCEn面积为S1、S2、S3、…Sn. 则Sn= SABC( 用含n的代数式表示).
用含n的代数式表示).
某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元.
(1)该顾客至少可得到 元购物券,至多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
某校初二全体320名学生在参加电脑培训前后各进行了一次水平相同的考试,考试都以同一标准划分成“不合格、合格、优秀”三个等级,为了了解培训的效果,用抽签的方式得到其中32名学生的两次考试等级,所绘的统计图如图所示,结合图示信息回答下列问题: ⑴这32名学生培训前考分的中位数所在的等级是 ;⑵这32名学生经过培训后,考分等级“不合格”的百分比是 ;⑶估计该校整个初二年级中,培训后考分等级为“合格”与“优秀”的学生共有 名;⑷你认为上述估计合理吗?理由是什么?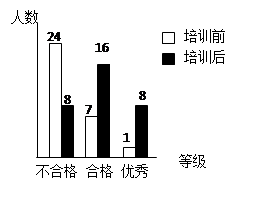
如图,一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度?(保留根号)
甲乙两人同时登山,甲、乙两人距地面的高度 (米)与登山时间
(米)与登山时间 之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,乙在 地提速时距地面的高度
地提速时距地面的高度 为 ____米;
为 ____米;
(2)若乙提速后,乙的速度是甲登山速度的3倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度 (米)与登山时间
(米)与登山时间 之间的函数关系式;
之间的函数关系式;
(3)登山多长时间时,乙追上了甲?
如图,AB是⊙O的直径,BC是弦,∠ABC的平分线BD交⊙O于点D,DE⊥BC,交BC的延长线于点E,BD交AC于点F.⑴求证:DE是⊙O的切线;(2) 若CE=1,ED=2,求⊙O的半径.
某公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润(万元)与投资金额 (万元)之间满足正比例函数关系:
(万元)之间满足正比例函数关系: ;如果单独投资B种产品,则所获利润(万元)与投资金额
;如果单独投资B种产品,则所获利润(万元)与投资金额 (万元)之间满足二次函数关系:
(万元)之间满足二次函数关系: .根据公司信息部的报告,
.根据公司信息部的报告, ,
, (万元)与投资金额
(万元)与投资金额 (万元)的部分对应值如下表所示:
(万元)的部分对应值如下表所示:
 |
1 |
5 |
 |
0.8 |
4 |
 |
3.8 |
15 |
(1)填空: ;
; ;
;
(2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为w(万元),试写出w与某种产品的投资金额x之间的函数关系式;
(3)请你设计一个在⑵中能获得最大利润的投资方案.
如果一个点能与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A,B两点可构成直角三角形ABC,则称点C为A,B两点的勾股点.同样,点D也是A,B两点的勾股点.
(1)如图1,矩形ABCD中,AB=2,BC=1,请在边CD上作出A,B两点的勾股点(点C和点D除外)(要求:尺规作图,保留作图痕迹,不要求写作法);
(2)矩形ABCD中,AB=3,BC=1,直接写出边CD上A, B两点的勾股点的个数;
(3)如图2,矩形ABCD中,AB=12,BC=4,DP=4,DM=8,AN=5.过点P作直线l平行于BC,点H为M,N两点的勾股点,且点H在直线l上.求PH的长.
根据国家统计局的公布数据,2010年我国GDP的总量约为398 000亿元人民币
将398 000 用科学记数法表示应为
| A.398×103 | B.0.398×106 | C.3.98×105 | D. 3.98×106 |
如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于
| A.30° | B.40° | C.60° | D.70° |
如图,在△ABC中,D、E分别是BC、AC边的中点.若DE=2,则AB的长度是
A.6 B.5 C.4 D.3
甲、乙、丙、丁四名学生10次小测验成绩的平均数(单位:分)和方差如下表:
| 选 手 |
甲 |
乙 |
丙 |
丁 |
| 平均数 |
92 |
92 |
92 |
92 |
| 方差 |
0.035 |
0.015 |
0.025 |
0.027 |
则这四人中成绩最稳定的是
A.甲 B.乙 C.丙 D.丁
已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于
A.11 |
B.10 |
C.9 |
D.8 |
若从10~99这连续90个正整数中选出一个数,其中每个数被选出的机会相等,则选出的
数其十位数字与个位数字的和为9的概率是
A. |
B. |
C. |
D. |
如图,在矩形ABCD中,AB=5,BC=4,E、F分别是AB、AD的中点.动点从点B出发,沿B→C→D→F方向运动至点处停止.设点运动的路程为,的面积为,当取到最大值时,点应运动到
A.的中点处 B.点处
C.的中点处 D.点处
已知A、B是抛物线y=x2-4x+3上关于对称轴对称的两点,则A、B的坐标可能
是 .(写出一对即可)
如图,直线  ,点
,点  坐标为(1,0),过点
坐标为(1,0),过点  作
作  轴的垂线交直线于点
轴的垂线交直线于点  ,以原点
,以原点  为圆心,
为圆心,  长为半径画弧交
长为半径画弧交  轴于点
轴于点  ;再过点
;再过点  作
作  轴的垂线交直线于点
轴的垂线交直线于点  ,以原点
,以原点  为圆心,
为圆心,  长为半径画弧交
长为半径画弧交  轴于点
轴于点  ,…,按此做法进行下去,点
,…,按此做法进行下去,点  的坐标为( , );点
的坐标为( , );点  ( , ).
( , ). 
如图,在四边形ABCD中, AC是∠DAE的平分线,DA∥CE,∠AEB=∠CEB. 求证:AB="CB." 
随着人们节能意识的增强,节能产品进入千家万户,今年1月小明家将天燃气热水器换成了太阳能热水器.去年12月份小明家的燃气费是96元,从今年1月份起天燃气价格每立方米上涨25%,小明家2月份的用气量比去年12月份少10立方米,2月份的燃气费是90元.问小明家2月份用气多少立方米.
如图,在平行四边形 中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.
中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.
(1)求证: ∠BAE=∠DAF;
∠BAE=∠DAF;
(2)若AE=4,AF= ,
, ,求CF的长.
,求CF的长.
某中学的地理兴趣小组在本校学生中开展主题为“地震知识知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:
| 等级 |
非常了解 |
比较了解 |
基本了解 |
不太了解 |
| 频数 |
40 |
120 |
n |
4 |
| 频率 |
0.2 |
m |
0.18 |
0.02 |
(1)表中的m的值为_______,n的值为 .
(2)根据表中的数据,请你计算“非常了解”的频率在下图中所对应的扇形的圆心角的度数,并补全扇形统计图.
(3)若该校有1500名学生,请根据调查结果估计这些学生中“比较了解”的人数约为多少?
已知:AB是⊙O的弦,OD⊥AB于M交⊙O于点D,CB⊥AB交AD的延长线于C.
(1)求证:AD=DC;
(2)过D作⊙O的切线交BC于E,若DE=2,CE=1,求⊙O的半径.
在平面直角坐标系xOy中,一次函数y=k x+b与反比例函数y=
x+b与反比例函数y= 的图象交于A(1,6),B(a,3)两点 .
的图象交于A(1,6),B(a,3)两点 .
(1)求k , k
, k 的值;
的值;
(2)如图,点D在x轴上,在梯形OBCD中,BC∥OD,OB=DC,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为18时,求PE:PC的值.
如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长.
小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
(1)请你帮小萍求出x的值.
(2) 参考小萍的思路,探究并解答新问题:
如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
已知关于x的方程(m-1)x2-(2m-1)x+2=0有两个正整数根.
(1) 确定整数m值;
(2) 在(1)的条件下,利用图象写出方程(m-1)x2-(2m-1)x+2+ =0的实数根的个数.
=0的实数根的个数.
等边△ABC边长为6,P为BC边上一点,∠MPN=60°,且PM、PN分别于边AB、AC交于点E、F.
(1)如图1,当点P为BC的三等分点,且PE⊥AB时,判断△EPF的形状;
(2)如图2,若点P在BC边上运动,且保持PE⊥AB,设BP=x,四边形AEPF面积的y,求y与x的函数关系式,并写出自变量x的取值范围;
(3)如图3,若点P在BC边上运动,且∠MPN绕点P旋转,当CF=AE=2时,求PE的长.
如图,已知二次函数y=ax2+bx+8(a≠0)的图像与x轴交于点A(-2,0),B,与y轴交于点C,tan∠ABC=2.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
 = .
= .

 的顶点
的顶点 作直线
作直线 ,过
,过 作
作 .若
.若 ,
, ,则
,则 的长度为 .
的长度为 .
 +
+ ;
;  时,求代数式
时,求代数式 的值.
的值.


 有意义,则
有意义,则 的取值范围是____________.
的取值范围是____________. .
. 的整数解.
的整数解. ,其中
,其中 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号