甲乙两人同时登山，甲、乙两人距地面的高度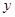
（米）与登山时间
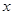之间的函数图象如图所示，根据图象所提供的信息解答下列问题：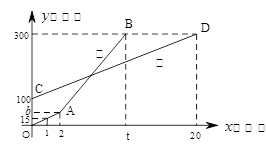
（1）甲登山的速度是每分钟 米，乙在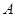
地提速时距地面的高度
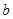为 ____米；
（2）若乙提速后，乙的速度是甲登山速度的3倍，请分别求出甲、乙二人登山全过程中，登山时距地面的高度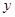（米）与登山时间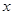之间的函数关系式；
（3）登山多长时间时，乙追上了甲？
，其中 
。
。
时，由于粗心，误认为加上此式，得到的结果为
，试求此题的正确结果。
－1）2＝0，问单项式3x2ym＋n－1和 x2m－n＋1y4是同类项吗？相关知识点
推荐套卷
甲乙两人同时登山，甲、乙两人距地面的高度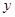（米）与登山时间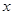之间的函数图象如图所示，根据图象所提供的信息解答下列问题：
（1）甲登山的速度是每分钟 米，乙在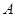地提速时距地面的高度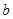为 ____米；
（2）若乙提速后，乙的速度是甲登山速度的3倍，请分别求出甲、乙二人登山全过程中，登山时距地面的高度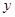（米）与登山时间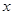之间的函数关系式；
（3）登山多长时间时，乙追上了甲？
粤公网安备 44130202000953号