广东省初中数学竞赛题
如图,是一块钜形 的场地,长
的场地,长 =101米,宽
=101米,宽 =52米,从
=52米,从 、
、 两处入口的中路宽都为1米,两小路汇合处路口宽为2米,其余部分种植草坪面积为___米2
两处入口的中路宽都为1米,两小路汇合处路口宽为2米,其余部分种植草坪面积为___米2
某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知地毯每平方米40元,主楼梯道的宽为3米,问买地毯至少需要多少元? 
如图,若要在长32m,宽20m的长方形地面上修筑同样宽2米的两条道路,余下的部分修草坪,草坪的面积是多少?
如图,把直角梯形 沿
沿 方向平移得到梯形
方向平移得到梯形 ,
, 与
与 相交于点
相交于点 ,
, =20cm,
=20cm, =5cm,
=5cm, =4cm,图中阴影部分的面积与哪个四边形的面积相等,并求出阴影部分的面积
=4cm,图中阴影部分的面积与哪个四边形的面积相等,并求出阴影部分的面积
.下列现象中,属于平移现象的为( )
| A.方向盘的转动 | B.自行车行驶时车轮的转动 | C.钟摆的运动 | D.电梯的升降 |
如图所示,某战役 缴获敌人
缴获敌人 防御工事坐标地图碎片,依稀可见:一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,2)。另有情报得知:指挥部坐标为(0,0),你认为敌军指挥部的位置大约是( )
防御工事坐标地图碎片,依稀可见:一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,2)。另有情报得知:指挥部坐标为(0,0),你认为敌军指挥部的位置大约是( )
| A.A处 | B.B处 | C.C处 | D.D处 |
将△ABC的各点的横坐标都加上3,纵坐标不变,所得图形与原图形相比( )
| A.向右平移了3个单位 | B.向左平移了3个单位 | C.向上平移了3个单位 | D.向下平移了3个单位 |
在平面直角坐标系中,已知线段AB的两个端点分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A′B′,若点A′的坐标为(-2,2)则点B′的坐标为( )
| A.(4,3) | B.(3,4) | C.(-1,-2) | D.(-2,-1) |
在平面直角坐标系中,将点P(-2,3) 沿X轴方向向右平移3个单位得到点Q,则点Q的坐标是 ( )
沿X轴方向向右平移3个单位得到点Q,则点Q的坐标是 ( )
A.(-2,6) B.(-2,0) C(-5,3 ) D.(1,3)
将点P(m+2,2m+4)向右平移1个单位得到P′,且P′在Y轴上, 那么P′坐标是()
那么P′坐标是()
| A.(-2,0) | B.(0,-2) | C.(1,0) | D. (0,1) (0,1) |
点P位于x轴下方,距离x轴5个单位 ,位于y轴右方,距离y轴3个单位,那么P点的坐标是( )
,位于y轴右方,距离y轴3个单位,那么P点的坐标是( )
| A.(5,-3) | B.(3,-5) | C.(-5,3) | D.(-3,5) |
将点B(5,-1)向上平移2个单位得到点A(a+b, a-b)。则( )
| A.a=2, b=3 | B.a=3, b=2 | C.a=-3, b=-2 | D.a=-2, b=-3 |
已知点A(3-p,2+p)先向x轴负方向平移2个单位,再 向y轴负方向平移3个单位得点B(p,-p),则点B的具体坐标为( )
向y轴负方向平移3个单位得点B(p,-p),则点B的具体坐标为( )
A. |
B. |
C. |
D. |
将点A(p, q) (p>0,q>0)向下平移p个单位,再向左平移q个单位得到点B,则点B的坐标为( )
| A.(0, 0) | B.(2p, 0) | C.(0,2q) | D.(p-q, q-p) |
小红家在电视塔西北200米处,小亮家在电视塔西南200米处,则小红家在小亮家的_______方向
已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2011的值为
点P(-5,1)沿x轴正方向平移2个单位,在沿y轴负方向平移4个单位所得的点的坐标为
已知点A(a,5)、B(2,2-b)、C(4,2)且AB平行x轴AC平行于y轴,则a + b=
一条船由原点O出发航行,先向东航行10千米到A点,接着又向北航行20千米至B点,最后又向东航行15千米至C点,则C点的坐标为 。
在平面直角坐标系中,将线段AB平移到A′B′,若点A、B、A′的坐标分别是(-2,0),(0,3),(2,1),则点B′的坐标是__
将点A(3,-4)沿X轴负方向平移3个单位长度,得到A′点的坐标为_,再将A′沿Y轴正方向平移4个单位长度,得到A″ 点的坐标为_
点的坐标为_
如图,点A坐标为(-1,1),将此小船向左平移2个单位后,画出图形,并指出A,B,C,D各点坐标.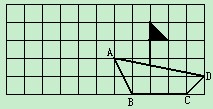
已知:矩形ABCD的顶点坐标为A(1,1),B(2,1),C(2,3),D(1,3)在平面直角坐标系标出个点。
(1)将矩形向上平移2个单位,画出相应的图形,并写出各点的坐标;
(2)将矩形各顶点的横、纵坐标都乘以-1,画出相应的图形;
(3)在(1)、(2)中,你发现了什么?
小红是某中学的七年级学生,放学后从学校骑自行车回家,学校在她现在位置的北偏东30°方向,距离此处1.5km的地方,她的家在她现在的位置的南偏西45°的方向,距离此处2km,邮局在她现在的位置的北偏西60°的方向,距离此处3km。根据这些信息画一张表示各处位置的简图
如图 (1) ,将平行四边形ABCD向左平移2个单位长度,可以得到A’B’C’D’,画出平移后的图形,并指出其各个顶点的坐标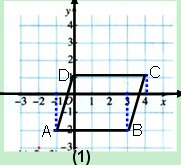
如图
(1)请写出在直角坐标系中的房子的A、B、C、D、E、F、G的坐标。
(2)源源想把房子向下平移3个单位长度,你能帮他办到吗?请作出相应图案,并写出平移后的7个点的坐标。
小明的爸爸早晨出去散步,从家走了20分到达距离家800米的公园,他在公园休息了10分,然后用30分原路返回家中,那么小明的爸爸离家的距离S(单位:米)与离家的时间t(单位:分)之间的函数关系图象大致是( )
已知抛物线C: ,将抛物线C平移得到抛物线C,若两条抛物线C、C关于直线x=1对称,则下列平移方法中,正确的是( )
,将抛物线C平移得到抛物线C,若两条抛物线C、C关于直线x=1对称,则下列平移方法中,正确的是( )
(A)将抛物线C向右平移 个单位 (B)将抛物线C向右平移3个单位
个单位 (B)将抛物线C向右平移3个单位
(C)将抛物线C向右平移5个单位 (D)将抛物线C向右平移6个单位
在一个不透明的盒子里,装有10个红球和5个蓝球,它们除颜色不同外,其余均相同,从中随机摸出一个球,它为蓝球的概率是( )
A. |
B. |
C. |
D. |
如图,点A、B、P在⊙O上,且∠APB=50°,若点M是⊙O上的动点,要使ABM为等腰三角形,则所有符合条件的点M有( )
(A)1个 (B)2个 (C)3个 (D)4个
若(2,k)是双曲线 上的一点,则函数
上的一点,则函数 的图象经过( )
的图象经过( )
| A.第一、三象限 | B.第二、四象限 | C.第一、二象限 | D.第三、四象限 |
如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N,给出以下三个结论:①MN∥AB;② =
= +
+ ;③MN≤
;③MN≤ AB,其中正确结论的个数是( )
AB,其中正确结论的个数是( )
A.0 B.1 C.2 D.3
若自然数n使得三个数的加法运算“”产生进位现象,则称n为“连加进位数”,例如,2不是“连加进位数”,因为2+3+4=9不产生进位现象;4是“连加进位数”,因为4+5+6=15产生进位现象;13是“连加进位数”,因为13+14+15=42产生进位现象;51是“连加进位数”,因为51+52+53=156产生进位现象.如果从0,1,2,99这100个自然数中任取一个数,那么取到“连加进位数”的概率是( )
| A.0.88 | B.0.89 | C.0.90 | D.0.91 |
△ABC中,已知BD和CE分别是两边上的中线,并且BD⊥CE,BD=4,CE=6,
那么ABC的面积等于( )
| A.12 | B.14 | C.16 | D.18 |
某城市按以下规定收取每月煤气费:每月所用煤气按整立方米数计算;若每月用煤气不超过60立方米,按每立方米0.8元收费;若超过60立方米,超过部分按每立方米1.2元收费.已知某户人家某月的煤气费平均每立方米0.88元,则这户人家需要交煤气费
| A.60元 | B.66元 | C.75元 | D.78元 |
如图,在△ABC中,D是BC上的一点,已知AC=5,AD=6,BD=10,CD=5,则△ABC的面积是( )
| A.30 | B.36 | C.72 | D.125 |
若实数 满足条件
满足条件 ,则
,则 中( )
中( )
| A.必有两个数相等 | B.必有两个数互为相反的数 |
| C.必有两个数互为倒数 | D.每两个数都不等 |
平面直角坐标系中,若一个点的横、纵坐标都是整数,则称该点为整点.若
函数的图象的交点为整点时,则整数k的值可取( )
| A.2个 | B.3个 | C.4个 | D.5个 |
A、B两站间特快列车需要行驶3小时30分钟,早6时两站同时对发首次列车,以后每隔1小时发一次车.那么,上午9时从A站发出的特快列车将与B站出发的列车相遇的次数是( )
(A)5次 (B)6次 (C)7次 (D)8次
 沿
沿 方向平移
方向平移 距离得到
距离得到 ,已知
,已知 =5,
=5, =8,
=8, =3,求图中阴影部分面积。
=3,求图中阴影部分面积。
 的图象,当
的图象,当 时,随的增大而增大,则的取值范围是
时,随的增大而增大,则的取值范围是








 的解集是( )
的解集是( )




 都是实数,并且
都是实数,并且 ,那么下列式子中正确的是( )
,那么下列式子中正确的是( )



 有实数根且它的两根之差是1,那么p的值为
有实数根且它的两根之差是1,那么p的值为

 的图象如图所示,有下列4个结论,其中正确的结论是( )
的图象如图所示,有下列4个结论,其中正确的结论是( )


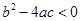
 为实数,
为实数, 一定等于( )
一定等于( )



 的值等于( )
的值等于( )


 满足
满足 则
则 的最小值为( )
的最小值为( )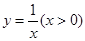 的图象上,则点E的坐标是( )
的图象上,则点E的坐标是( )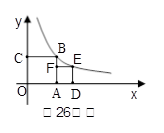
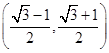
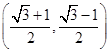
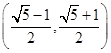
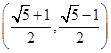
 为,则此等腰三角形的底长为( )
为,则此等腰三角形的底长为( )




 粤公网安备 44130202000953号
粤公网安备 44130202000953号