如图,已知抛物线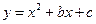 经过
经过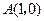 ,
, 两点,顶点为
两点,顶点为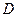 .
.
(1)求抛物线的解析式;
(2)将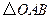 绕点
绕点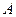 顺时针旋转90°后,点
顺时针旋转90°后,点 落到点
落到点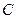 的位置,将抛物线沿
的位置,将抛物线沿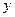 轴平移后经过点
轴平移后经过点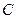 ,求平移后所得图象的函数关系式;
,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与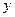 轴的交点为
轴的交点为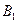 ,顶点为
,顶点为 ,若点
,若点 在平移后的抛物线上,且满足
在平移后的抛物线上,且满足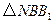 的面积是
的面积是 面积的2倍,求点
面积的2倍,求点 的坐标.
的坐标.
二次函数y=x2的图象向右平移3个单位,得到新的图象的函数表达式是( )
| A.y=x2+3 | B.y=x2-3 | C.y=(x+3)2 | D.y=(x-3)2 |
如图,已知 ,
, 是一次函数
是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.(1)求反比例函数和一次函数的解析式;(2)求直线
的图象的两个交点.(1)求反比例函数和一次函数的解析式;(2)求直线 与
与 轴的交点
轴的交点 的坐标及△
的坐标及△ 的面积;(3)求不等式
的面积;(3)求不等式 的解集(请直接写出答案).
的解集(请直接写出答案).
小颖同学想用“描点法”画二次函数 的图象,取自变量x的5个值,分别计算出对应的y值,如下表:
的图象,取自变量x的5个值,分别计算出对应的y值,如下表:
 |
… |
 |
 |
0 |
1 |
2 |
… |
 |
… |
11 |
2 |
-1 |
2 |
5 |
… |
由于粗心,小颖算错了其中的一个y值,请你指出这个算错的y值所对应的x=
二次函数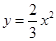 的图像如图所示,点
的图像如图所示,点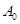 位于坐标原点,
位于坐标原点,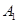 ,
, 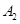 ,
,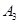 ,…,
,…, 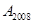 在y轴的正半轴上,
在y轴的正半轴上,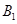 ,
,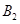 ,
,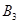 ,…,
,…, 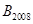 在二次函数
在二次函数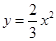 第一象限的图像上,若△
第一象限的图像上,若△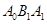 ,△
,△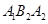 ,△
,△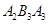 ,…,△
,…,△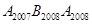 都为等边三角形,请计算△
都为等边三角形,请计算△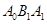 的边长= ;△
的边长= ;△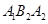 的边长= ;△
的边长= ;△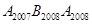 的边长=
的边长= 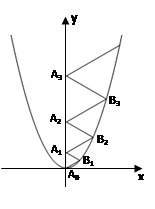
已知反比例函数y=的图象与二次函数y=ax2+x-1的图象相交于点(2,2)
(1)求a和k的值;
(2)反比例函数的图象是否经过二次函数图象的顶点,为什么?
已知二次函数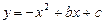 的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)。
的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)。
(1)求出b,c的值,并写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围
一条抛物线具有下列性质:(1)经过点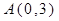 ;(2)在
;(2)在 轴左侧的部分是上升的,在
轴左侧的部分是上升的,在 轴右侧的部分是下降的. 试写出一个满足这两条性质的抛物线的表达式.
轴右侧的部分是下降的. 试写出一个满足这两条性质的抛物线的表达式.
已知抛物线 的开口向下,顶点坐标为(2,-3) ,那么该抛物线有( )
的开口向下,顶点坐标为(2,-3) ,那么该抛物线有( )
| A.最小值 -3 | B.最大值-3 | C.最小值2 | D.最大值2 |
如图9,抛物线 与
与 轴交于
轴交于 、
、 两点(点
两点(点 在点
在点 的左侧),抛物线上另有一点
的左侧),抛物线上另有一点 在第一象限,满足∠
在第一象限,满足∠ 为直角,且恰使△
为直角,且恰使△ ∽△
∽△ .
.
(1)(3分)求线段 的长.
的长.
(2)(3分)求该抛物线的函数关系式.
(3)(4分)在 轴上是否存在点
轴上是否存在点 ,使△
,使△ 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4) ,连接AE、ED.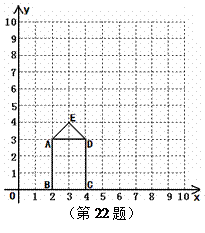
(1)求经过A、E、D三点的抛物线的解析式;
(2)以原点为位似中心,将五边形ABCDE放大.
① 若放大后的五边形的边长是原五边形对应边长的 2 倍,请在网格中画出放大后的五边形A2B2C2D2E2,并直接写出经过A2、E2、D2三点的抛物线的解析式: ;
② 若放大后的五边形的边长是原五边形对应边长的 k 倍,请你直接写出经过Ak、Ek、Dk三点的抛物线的解析式: .(用含k的字母表示)
某网站出售一种毛绒兔玩具,试销中发现这种玩具每个获利x元时,一天需销售(60-x)个,如果要使一天出售该种玩具获得最大销售利润,那么每个玩具应获利多少元?
已知二次函数y =" x2" -4x +3.
(1)用配方法将y =" x2" -4x +3化成y =" a(x" -h) 2 + k的形式;
(2)在所给的平面直角坐标系中,画出这个二次函数的图象;
(3)根据图象回答:当自变量x的取值范围满足什么条件时,y<0?