初中数学解直角三角形的应用-仰角俯角问题试题

鄂州市某校数学兴趣小组借助无人机测量一条河流的宽度．如图所示，一架水平飞行的无人机在处测得正前方河流的左岸处的俯角为，无人机沿水平线方向继续飞行50米至处，测得正前方河流右岸处的俯角为．线段的长为无人机距地面的铅直高度，点、、在同一条直线上．其中，米．

（1）求无人机的飞行高度；（结果保留根号）

（2）求河流的宽度．（结果精确到1米，参考数据：，

某校为检测师生体温，在校门安装了某型号测温门．如图为该测温门截面示意图，已知测温门 $\mathit{AD}$ 的顶部 $A$ 处距地面高为 $2.2m$ ，为了解自己的有效测温区间．身高 $1.6m$ 的小聪做了如下实验：当他在地面 $N$ 处时测温门开始显示额头温度，此时在额头 $B$ 处测得 $A$ 的仰角为 $18°$ ；在地面 $M$ 处时，测温门停止显示额头温度，此时在额头 $C$ 处测得 $A$ 的仰角为 $60°$ ．求小聪在地面的有效测温区间 $\mathit{MN}$ 的长度．（额头到地面的距离以身高计，计算精确到 $0.1m$ ， $\sin 18°\approx 0.31$ ， $\cos 18°\approx 0.95$ ， $\tan 18°\approx 0.32)$

脱贫攻坚工作让老百姓过上了幸福的生活．如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高所在的直线，为了测量房屋的高度，在地面上点测得屋顶的仰角为，此时地面上点、屋檐上点、屋顶上点三点恰好共线，继续向房屋方向走到达点时，又测得屋檐点的仰角为，房屋的顶层横梁，，交于点（点，，在同一水平线上）．（参考数据：，，，

（1）求屋顶到横梁的距离；

（2）求房屋的高（结果精确到．

如图，，为两个建筑物，两建筑物底部之间的水平地面上有一点，从建筑物的顶点测得点的俯角为，从建筑物的顶点测得点的俯角为，测得建筑物的顶点的俯角为．若已知建筑物的高度为20米，求两建筑物顶点、之间的距离（结果精确到，参考数据：，．

如图，在处利用测角仪测得某建筑物的顶端点的仰角为，点的仰角为，点到建筑物的距离为米，则　　米．

襄阳卧龙大桥横跨汉江，是我市标志性建筑之一．某校数学兴趣小组在假日对竖立的索塔在桥面以上的部分（上塔柱和塔冠进行了测量．如图所示，最外端的拉索的底端到塔柱底端的距离为，拉索与桥面的夹角为，从点出发沿方向前进，在处测得塔冠顶端的仰角为．请你求出塔冠的高度（结果精确到．参考数据，，，．

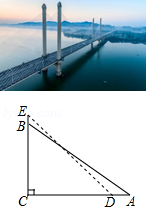
如图，为测量旗杆的高度，在教学楼一楼点处测得旗杆顶部的仰角为，在四楼点处测得旗杆顶部的仰角为，点与点在同一水平线上．已知，则旗杆的高度为　　．

如图，两座建筑物的水平距离为，从点测得点的俯角为，测得点的俯角为．求这两座建筑物，的高度．（结果保留小数点后一位，，．

如图，某地有甲、乙两栋建筑物，小明于乙楼楼顶点处看甲楼楼底点处的俯角为，走到乙楼点处看甲楼楼顶点处的俯角为，已知，．求乙楼的高度的长．（参考数据：，，精确到．

小强的爸爸准备驾车外出．启动汽车时，车载报警系统显示正前方有障碍物，此时在眼睛点 $A$ 处测得汽车前端 $F$ 的俯角为 $\alpha$ ，且 $\tan \alpha =\frac{1}{3}$ ，若直线 $\mathit{AF}$ 与地面 $l_1$ 相交于点 $B$ ，点 $A$ 到地面 $l_1$ 的垂线段 $\mathit{AC}$ 的长度为1.6米，假设眼睛 $A$ 处的水平线 $l_2$ 与地面 $l_1$ 平行．

（1）求 $\mathit{BC}$ 的长度；

（2）假如障碍物上的点 $M$ 正好位于线段 $\mathit{BC}$ 的中点位置（障碍物的横截面为长方形，且线段 $\mathit{MN}$ 为此长方形前端的边）， $\mathit{MN}\perp l_1$ ，若小强的爸爸将汽车沿直线 $l_1$ 后退0.6米，通过汽车的前端 $F_1$ 点恰好看见障碍物的顶部 $N$ 点（点 $D$ 为点 $A$ 的对应点，点 $F_1$ 为点 $F$ 的对应点），求障碍物的高度．

慈氏塔位于岳阳市城西洞庭湖边，是湖南省保存最好的古塔建筑之一．如图，小亮的目高为1.7米，他站在处测得塔顶的仰角为，小琴的目高为1.5米，她站在距离塔底中心点米远的处，测得塔顶的仰角为．（点、、在同一水平线上，参考数据：，，

（1）求小亮与塔底中心的距离；（用含的式子表示）

（2）若小亮与小琴相距52米，求慈氏塔的高度．

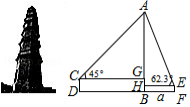
为了测量某山（如图所示）的高度，甲在山顶A测得C处的俯角为45°，D处的俯角为30°，乙在山下测得C，D之间的距离为400米．已知B，C，D在同一水平面的同一直线上，求山高AB．（可能用到的数据：1.414，1.732）

南洞庭大桥是南益高速公路上的重要桥梁，小芳同学在校外实践活动中对此开展测量活动．如图，在桥外一点 $A$ 测得大桥主架与水面的交汇点 $C$ 的俯角为 $\alpha$ ，大桥主架的顶端 $D$ 的仰角为 $\beta$ ，已知测量点与大桥主架的水平距离 $\mathit{AB}=a$ ，则此时大桥主架顶端离水面的高 $\mathit{CD}$ 为 $($ 　　 $)$

A．

$a\sin \alpha +a\sin \beta$

B．

$a\cos \alpha +a\cos \beta$

C．

$a\tan \alpha +a\tan \beta$

D．

$\frac{a}{\tan \alpha }+\frac{a}{\tan \beta }$

我国于2019年6月5日首次完成运载火箭海上发射，这标志着我国火箭发射技术达到了一个崭新的高度．如图，运载火箭从海面发射站点处垂直海面发射，当火箭到达点处时，海岸边处的雷达站测得点到点的距离为8千米，仰角为．火箭继续直线上升到达点处，此时海岸边处的雷达测得处的仰角增加，求此时火箭所在点处与发射站点处的距离．（结果精确到0.1千米）（参考数据：，

如图，在一次综合实践活动中，小亮要测量一楼房的高度，先在坡面处测得楼房顶部的仰角为，沿坡面向下走到坡脚处，然后向楼房方向继续行走10米到达处，测得楼房顶部的仰角为．已知坡面米，山坡的坡度（坡度是指坡面的铅直高度与水平宽度的比），求楼房高度．（结果精确到0.1米）（参考数据：，