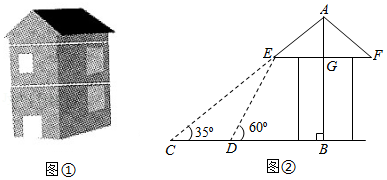
脱贫攻坚工作让老百姓过上了幸福的生活．如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高所在的直线，为了测量房屋的高度，在地面上点测得屋顶的仰角为，此时地面上点、屋檐上点、屋顶上点三点恰好共线，继续向房屋方向走到达点时，又测得屋檐点的仰角为，房屋的顶层横梁，，交于点（点，，在同一水平线上）．（参考数据：，，，
（1）求屋顶到横梁的距离；
（2）求房屋的高（结果精确到．
相关试题
如果
分别是一元二次方程
+
+
=0（≠0）的两根，请你解决下列问题：
（1）推导根与系数的关系：
＝-
，
＝
（2）已知
，
是方程-4+2=0的两个实根，利用根与系数的关系求
的值；
（3）已知sin，cos（
）是关于x的方程2-
的两个根，求角的度数．
2013年10月31日20时02分在台湾花莲县，发生6.7级地震，某地震救援队接到上级命令后立即赶赴震区进行救援。救援队利用生命探测仪在某建筑物废墟下方探测到点 C 处有生命迹象，已知废墟一侧地面上两探测点A、B 相距3米，探测线与地面夹角分别是30°和 60°（如图），试确定生命所在点 C 的深度。（结果精确到0.1米，参考数据：
）
，
，
，
…从计算结果中找出规律，并利用这一规律计算：
相关知识点
推荐套卷
粤公网安备 44130202000953号