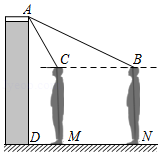
某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门 的顶部 处距地面高为 ,为了解自己的有效测温区间.身高 的小聪做了如下实验:当他在地面 处时测温门开始显示额头温度,此时在额头 处测得 的仰角为 ;在地面 处时,测温门停止显示额头温度,此时在额头 处测得 的仰角为 .求小聪在地面的有效测温区间 的长度.(额头到地面的距离以身高计,计算精确到 , , ,
相关知识点
推荐套卷
某校为检测师生体温,在校门安装了某型号测温门.如图为该测温门截面示意图,已知测温门 的顶部 处距地面高为 ,为了解自己的有效测温区间.身高 的小聪做了如下实验:当他在地面 处时测温门开始显示额头温度,此时在额头 处测得 的仰角为 ;在地面 处时,测温门停止显示额头温度,此时在额头 处测得 的仰角为 .求小聪在地面的有效测温区间 的长度.(额头到地面的距离以身高计,计算精确到 , , ,
