初中数学解直角三角形解答题

用如图①，②所示的两个直角三角形（部分边长及角的度数在图中已标出），完成以下两个探究问题：

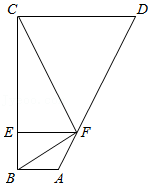
探究一：将以上两个三角形如图③拼接（BC和ED重合），在BC边上有一动点P．
（1）当点P运动到∠CFB的角平分线上时，连接AP，求线段AP的长；
（2）当点P在运动的过程中出现PA=FC时，求∠PAB的度数．
探究二：如图④，将△DEF的顶点D放在△ABC的BC边上的中点处，并以点D为旋转中心旋转△DEF，使△DEF的两直角边与△ABC的两直角边分别交于M、N两点，连接MN．在旋转△DEF的过程中，△AMN的周长是否存在有最小值？若存在，求出它的最小值；若不存在，请说明理由．

如图，点A，B，C表示某旅游景区三个缆车站的位置，线段AB，BC表示连接缆车站的钢缆，已知A，B，C三点在同一铅直平面内，它们的海拔高度AA′，BB′，CC′分别为110米、310米、710米，钢缆AB的坡度i1=1：2，钢缆BC的坡度i2=1：1．景区因改造缆车线路，需要从A到C直线架设一条钢缆，那么钢缆AC的长度是多少米？（注：坡度是指坡面的铅直高度与水平宽度的比．）

（1）如图①，若BC=6，AC=4，∠C=60°，求△ABC的面积S_△ABC；
（2）如图②，若BC=a，AC=b，∠C=α，求△ABC的面积S_△ABC；
（3）如图③，四边形ABCD，若AC=m，BD=n，对角线AC、BD交于O点，它们所成的锐角为β．求四边形ABCD的面积S_{四边形ABCD} ．

如图，在射线 $\mathit{BA}$， $\mathit{BC}$， $\mathit{AD}$， $\mathit{CD}$围成的菱形 $\mathit{ABCD}$中， $\angle \mathit{ABC}=60°$， $\mathit{AB}=6\sqrt{3}$， $O$是射线 $\mathit{BD}$上一点， $\odot O$与 $\mathit{BA}$， $\mathit{BC}$都相切，与 $\mathit{BO}$的延长线交于点 $M$．过 $M$作 $\mathit{EF}\perp \mathit{BD}$交线段 $\mathit{BA}$（或射线 $\mathit{AD})$于点 $E$，交线段 $\mathit{BC}$（或射线 $\mathit{CD})$于点 $F$．以 $\mathit{EF}$为边作矩形 $\mathit{EFGH}$，点 $G$， $H$分别在围成菱形的另外两条射线上．

（1）求证： $\mathit{BO}=2\mathit{OM}$．

（2）设 $\mathit{EF}>\mathit{HE}$，当矩形 $\mathit{EFGH}$的面积为 $24\sqrt{3}$时，求 $\odot O$的半径．

（3）当 $\mathit{HE}$或 $\mathit{HG}$与 $\odot O$相切时，求出所有满足条件的 $\mathit{BO}$的长．

如图1，△ABC中，CA=CB，点O在高CH上，OD⊥CA于点D，OE⊥CB于点E，以O为圆心，OD为半径作⊙O．

（1）求证：⊙O与CB相切于点E；
（2）如图2，若⊙O过点H，且AC=5，AB=6，连接EH，求△BHE的面积和tan∠BHE的值．

2013年4月20日，四川雅安发生里氏7.0级地震，救援队救援时，利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象，已知废墟一侧地面上两探测点A、B相距4米，探测线与地面的夹角分别为30⁰和60⁰，如图所示，试确定生命所在点C的深度（结果精确到0.1米，参考数据≈1.41，≈1.73）

如图，防洪大堤的横断面是梯形ABCD，其中AD∥BC，坡角α=60⁰，汛期来临前对其进行了加固，改造后的背水面坡角β=45⁰，若原坡长AB=20m，求改造后的坡长AE（结果保留根号）

如图，在平面直角坐标系中， $O$为坐标原点，点 $A$的坐标为 $(5,0)$，菱形 $\mathit{OABC}$的顶点 $B$， $C$都在第一象限， $\tan \angle \mathit{AOC}=\frac{4}{3}$，将菱形绕点 $A$按顺时针方向旋转角 $\alpha (0°<\angle \alpha <\angle \mathit{AOC})$得到菱形 $\mathit{FADE}$（点 $O$的对应点为点 $F)$， $\mathit{EF}$与 $\mathit{OC}$交于点 $G$，连接 $\mathit{AG}$．

（1）求点 $B$的坐标．

（2）当 $\mathit{OG}=4$时，求 $\mathit{AG}$的长．

（3）求证： $\mathit{GA}$平分 $\angle \mathit{OGE}$．

（4）连接 $\mathit{BD}$并延长交 $x$轴于点 $P$，当点 $P$的坐标为 $(12,0)$时，求点 $G$的坐标．

如图所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在图的半径的活动。小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，求小桥所在圆的半径。

如图，大海中有A和B两个岛屿，为测量它们之间的距离，在海岸线PQ上点E处测得∠AEP＝74°，∠BEQ＝30°；在点F处测得∠AFP＝60°，∠BFQ＝60°，EF＝1km．

（1）判断线段AB与AE的数量关系，并说明理由；
（2）求两个岛屿A和B之间的距离（结果精确到0.1km）．

如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，∠CBA=32°，求∠EFD的度数。    

海中两个灯塔A、B，其中B位于A的正东方向上，渔船跟踪鱼群由西向东航行，在点C处测得灯塔A在西北方向上，灯塔B在北偏东30°方向上，渔船不改变航向继续向东航行30海里到达点D，这是测得灯塔A在北偏西60°方向上，求灯塔A、B间的距离．（计算结果用根号表示，不取近似值）

如图，在四边形 $\mathit{ABCD}$中， $\mathit{AB}//\mathit{CD}$， $\mathit{AB}\ne \mathit{CD}$， $\angle \mathit{ABC}=90°$，点 $E$、 $F$分别在线段 $\mathit{BC}$、 $\mathit{AD}$上，且 $\mathit{EF}//\mathit{CD}$， $\mathit{AB}=\mathit{AF}$， $\mathit{CD}=\mathit{DF}$．

（1）求证： $\mathit{CF}\perp \mathit{FB}$；

（2）求证：以 $\mathit{AD}$为直径的圆与 $\mathit{BC}$相切；

（3）若 $\mathit{EF}=2$， $\angle \mathit{DFE}=120°$，求 $\mathit{\Delta ADE}$的面积．

如图，在平面直角坐标系中，二次函数的图象与一次函数的图象交于A、B两点，点A在x轴上，点B的纵坐标为．点P是二次函数图象上A、B两点之间的一个动点（不与点A、B重合），设点P的横坐标为m，过点P作x轴的垂线交AB于点C，作PD⊥AB于点D．

（1）求b及sin∠ACP的值；
（2）用含m的代数式表示线段PD的长；
（3）连接PB，线段PC把△PDB分成两个三角形，是否存在适合的m值，使这两个三角形的面积之比为．如果存在，直接写出m的值；如果不存在，请说明理由．

如图，直角 $\mathit{\Delta ABC}$中， $\angle A$为直角， $\mathit{AB}=6$， $\mathit{AC}=8$．点 $P$， $Q$， $R$分别在 $\mathit{AB}$， $\mathit{BC}$， $\mathit{CA}$边上同时开始作匀速运动，2秒后三个点同时停止运动，点 $P$由点 $A$出发以每秒3个单位的速度向点 $B$运动，点 $Q$由点 $B$出发以每秒5个单位的速度向点 $C$运动，点 $R$由点 $C$出发以每秒4个单位的速度向点 $A$运动，在运动过程中：

（1）求证： $\mathit{\Delta APR}$， $\mathit{\Delta BPQ}$， $\mathit{\Delta CQR}$的面积相等；

（2）求 $\mathit{\Delta PQR}$面积的最小值；

（3）用 $t$（秒 $\left)\right(0⩽t⩽2)$表示运动时间，是否存在 $t$，使 $\angle \mathit{PQR}=90°$？若存在，请直接写出 $t$的值；若不存在，请说明理由．