海中两个灯塔A、B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这是测得灯塔A在北偏西60°方向上,求灯塔A、B间的距离.(计算结果用根号表示,不取近似值)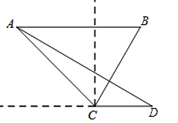
相关知识点
推荐套卷
海中两个灯塔A、B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这是测得灯塔A在北偏西60°方向上,求灯塔A、B间的距离.(计算结果用根号表示,不取近似值)