如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.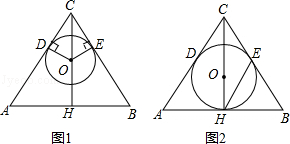
(1)求证:⊙O与CB相切于点E;
(2)如图2,若⊙O过点H,且AC=5,AB=6,连接EH,求△BHE的面积和tan∠BHE的值.
推荐套卷
如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.
(1)求证:⊙O与CB相切于点E;
(2)如图2,若⊙O过点H,且AC=5,AB=6,连接EH,求△BHE的面积和tan∠BHE的值.