初中数学解直角三角形解答题

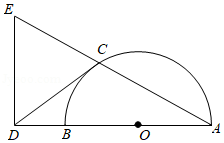
如图是放在水平地面上的一把椅子的侧面图，椅子高为AC，椅面宽为BE，椅脚高为ED，且AC⊥BE，AC⊥CD，AC∥ED．从点A测得点D、E的俯角分别为64°和53°．已知ED=35cm，求椅子高AC约为多少？

（参考数据：tan53°≈，sin53°≈，tan64°≈2，sin64°≈）

如图1，在菱形 $\mathit{ABCD}$中， $\mathit{AB}=6\sqrt{5}$， $\tan \angle \mathit{ABC}=2$，点 $E$从点 $D$出发，以每秒1个单位长度的速度沿着射线 $\mathit{DA}$的方向匀速运动，设运动时间为 $t$（秒 $)$，将线段 $\mathit{CE}$绕点 $C$顺时针旋转一个角 $\alpha (\alpha =\angle \mathit{BCD})$，得到对应线段 $\mathit{CF}$．

（1）求证： $\mathit{BE}=\mathit{DF}$；

（2）当 $t=$　       　秒时， $\mathit{DF}$的长度有最小值，最小值等于　          　；

（3）如图2，连接 $\mathit{BD}$、 $\mathit{EF}$、 $\mathit{BD}$交 $\mathit{EC}$、 $\mathit{EF}$于点 $P$、 $Q$，当 $t$为何值时， $\mathit{\Delta EPQ}$是直角三角形？

（4）如图3，将线段 $\mathit{CD}$绕点 $C$顺时针旋转一个角 $\alpha (\alpha =\angle \mathit{BCD})$，得到对应线段 $\mathit{CG}$．在点 $E$的运动过程中，当它的对应点 $F$位于直线 $\mathit{AD}$上方时，直接写出点 $F$到直线 $\mathit{AD}$的距离 $y$关于时间 $t$的函数表达式．

（本题10分）如图，从城市A到B城市的公路需经过城市C，图中AC=100千米，∠CAB=25°，∠CBA=37°，因城市规划的需要，将在A、B两城市间修建一条笔直的公路．

（1）求改直的公路AB的长；
（2）问公路改直后比原来缩短了多少千米？
（参考数据：sin25°≈0．42，cos25°≈0．91，sin37°≈0．60，tan37°≈0．75）

小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究．

（一猜测探究

在中，，是平面内任意一点，将线段绕点按顺时针方向旋转与相等的角度，得到线段，连接．

（1）如图1，若是线段上的任意一点，请直接写出与的数量关系是　　，与的数量关系是　　；

（2）如图2，点是延长线上点，若是内部射线上任意一点，连接，（1）中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由．

（二拓展应用

如图3，在△中，，，，是上的任意点，连接，将绕点按顺时针方向旋转，得到线段，连接．求线段长度的最小值．

（本题6+6分）
（1）计算：; 
（2）先化简，再求值：，其中x是方程的根．

如图，四边形 $\mathit{ABCD}$ 内接于 $\odot O$ ， $\angle 1=\angle 2$ ，延长 $\mathit{BC}$ 到点 $E$ ，使得 $\mathit{CE}=\mathit{AB}$ ，连接 $\mathit{ED}$ ．

（1）求证： $\mathit{BD}=\mathit{ED}$ ；

（2）若 $\mathit{AB}=4$ ， $\mathit{BC}=6$ ， $\angle \mathit{ABC}=60°$ ，求 $\tan \angle \mathit{DCB}$ 的值．

（1）如图1，菱形的顶点、在菱形的边上，且，请直接写出的结果（不必写计算过程）

（2）将图1中的菱形绕点旋转一定角度，如图2，求；

（3）把图2中的菱形都换成矩形，如图3，且，此时的结果与（2）小题的结果相比有变化吗？如果有变化，直接写出变化后的结果（不必写计算过程）；若无变化，请说明理由．

如图，在 $▱\mathit{ABCD}$ 中， $E$ ， $F$ 是对角线 $\mathit{BD}$ 上的两点（点 $E$ 在点 $F$ 左侧），且 $\angle \mathit{AEB}=\angle \mathit{CFD}=90°$ ．

（1）求证：四边形 $\mathit{AECF}$ 是平行四边形；

（2）当 $\mathit{AB}=5$ ， $\tan \angle \mathit{ABE}=\frac{3}{4}$ ， $\angle \mathit{CBE}=\angle \mathit{EAF}$ 时，求 $\mathit{BD}$ 的长．

如图，已知 $\mathit{AB}$ 是 $\odot O$ 的直径， $\angle \mathit{ACD}$ 是 $\widehat{\mathit{AD}}$ 所对的圆周角， $\angle \mathit{ACD}=30°$ ．

（1）求 $\angle \mathit{DAB}$ 的度数；

（2）过点 $D$ 作 $\mathit{DE}\perp \mathit{AB}$ ，垂足为 $E$ ， $\mathit{DE}$ 的延长线交 $\odot O$ 于点 $F$ ．若 $\mathit{AB}=4$ ，求 $\mathit{DF}$ 的长．

如图，已知点 $C$ 是以 $\mathit{AB}$ 为直径的半圆上一点， $D$ 是 $\mathit{AB}$ 延长线上一点，过点 $D$ 作 $\mathit{BD}$ 的垂线交 $\mathit{AC}$ 的延长线于点 $E$ ，连结 $\mathit{CD}$ ，且 $\mathit{CD}=\mathit{ED}$ ．

（1）求证： $\mathit{CD}$ 是 $\odot O$ 的切线；

（2）若 $\tan \angle \mathit{DCE}=2$ ， $\mathit{BD}=1$ ，求 $\odot O$ 的半径．

数学小组研究如下问题：长春市的纬度约为北纬 $44°$ ，求北纬 $44°$ 纬线的长度，小组成员查阅了相关资料，得到三条信息：

（1）在地球仪上，与南，北极距离相等的大圆圈，叫赤道，所有与赤道平行的圆圈叫纬线；

（2）如图， $\odot O$ 是经过南、北极的圆，地球半径 $\mathit{OA}$ 约为 $6400\mathit{km}$ ．弦 $\mathit{BC}//\mathit{OA}$ ，过点 $O$ 作 $\mathit{OK}\perp \mathit{BC}$ 于点 $K$ ，连接 $\mathit{OB}$ ．若 $\angle \mathit{AOB}=44°$ ，则以 $\mathit{BK}$ 为半径的圆的周长是北纬 $44°$ 纬线的长度；

（3）参考数据： $\pi$ 取3， $\sin 44°=0.69$ ， $\cos 44°=0.72$ ．

小组成员给出了如下解答，请你补充完整：

解：因为 $\mathit{BC}//\mathit{OA}$ ， $\angle \mathit{AOB}=44°$ ，

所以 $\angle B=\angle \mathit{AOB}=44°($ 　　 $)$ （填推理依据），

因为 $\mathit{OK}\perp \mathit{BC}$ ，所以 $\angle \mathit{BKO}=90°$ ，

在 $\text{Rt}\Delta \text{BOK}$ 中， $\mathit{OB}=\mathit{OA}=6400$ ．

$\mathit{BK}=\mathit{OB}\times$ 　　（填" $\sin B$ "或" $\cos B$ " $)$ ．

所以北纬 $44°$ 的纬线长 $C=2\pi \cdot \mathit{BK}$ ．

$=2\times 3\times 6400\times$ 　　（填相应的三角形函数值）

$\approx$ 　　 $\left(\mathit{km}\right)$ （结果取整数）．

如图，在 $\mathit{\Delta ABC}$中， $\angle \mathit{ACB}=90°$， $\mathit{AC}=m$， $\mathit{BC}=n$， $m>n$，点 $P$是边 $\mathit{AB}$上一点，连接 $\mathit{CP}$，将 $\mathit{\Delta ACP}$沿 $\mathit{CP}$翻折得到 $\mathit{\Delta QCP}$．

（1）若 $m=4$， $n=3$，且 $\mathit{PQ}\perp \mathit{AB}$，求 $\mathit{BP}$的长；

（2）连接 $\mathit{BQ}$，若四边形 $\mathit{BCPQ}$是平行四边形，求 $m$与 $n$之间的关系式．

如图1，在平面直角坐标系中，直线 $\mathit{MN}$分别与 $x$轴、 $y$轴交于点 $M(6,0)$， $N(0$， $2\sqrt{3})$，等边 $\mathit{\Delta ABC}$的顶点 $B$与原点 $O$重合， $\mathit{BC}$边落在 $x$轴正半轴上，点 $A$恰好落在线段 $\mathit{MN}$上，将等边 $\mathit{\Delta ABC}$从图1的位置沿 $x$轴正方向以每秒1个单位长度的速度平移，边 $\mathit{AB}$， $\mathit{AC}$分别与线段 $\mathit{MN}$交于点 $E$， $F$（如图2所示），设 $\mathit{\Delta ABC}$平移的时间为 $t\left(s\right)$．

（1）等边 $\mathit{\Delta ABC}$的边长为　　；

（2）在运动过程中，当 $t=$　　时， $\mathit{MN}$垂直平分 $\mathit{AB}$；

（3）若在 $\mathit{\Delta ABC}$开始平移的同时．点 $P$从 $\mathit{\Delta ABC}$的顶点 $B$出发．以每秒2个单位长度的速度沿折线 $\mathit{BA}-\mathit{AC}$运动．当点 $P$运动到 $C$时即停止运动． $\mathit{\Delta ABC}$也随之停止平移．

①当点 $P$在线段 $\mathit{BA}$上运动时，若 $\mathit{\Delta PEF}$与 $\mathit{\Delta MNO}$相似．求 $t$的值；

②当点 $P$在线段 $\mathit{AC}$上运动时，设 $S_{\mathit{\Delta PEF}}=S$，求 $S$与 $t$的函数关系式，并求出 $S$的最大值及此时点 $P$的坐标．

在 $\mathit{\Delta ABC}$中， $\mathit{AB}=\mathit{BC}$，点 $O$是 $\mathit{AC}$的中点，点 $P$是 $\mathit{AC}$上的一个动点（点 $P$不与点 $A$， $O$， $C$重合）．过点 $A$，点 $C$作直线 $\mathit{BP}$的垂线，垂足分别为点 $E$和点 $F$，连接 $\mathit{OE}$， $\mathit{OF}$．

（1）如图1，请直接写出线段 $\mathit{OE}$与 $\mathit{OF}$的数量关系；

（2）如图2，当 $\angle \mathit{ABC}=90°$时，请判断线段 $\mathit{OE}$与 $\mathit{OF}$之间的数量关系和位置关系，并说明理由

（3）若 $|\mathit{CF}-\mathit{AE}|=2$， $\mathit{EF}=2\sqrt{3}$，当 $\mathit{\Delta POF}$为等腰三角形时，请直接写出线段 $\mathit{OP}$的长．

如图，抛物线 $y=a{x}^2+\mathit{bx}-5(a\ne 0)$ 经过点 $A(4,-5)$ ，与 $x$ 轴的负半轴交于点 $B$ ，与 $y$ 轴交于点 $C$ ，且 $\mathit{OC}=5\mathit{OB}$ ，抛物线的顶点为点 $D$ ．

（1）求这条抛物线的表达式；

（2）联结 $\mathit{AB}$ 、 $\mathit{BC}$ 、 $\mathit{CD}$ 、 $\mathit{DA}$ ，求四边形 $\mathit{ABCD}$ 的面积；

（3）如果点 $E$ 在 $y$ 轴的正半轴上，且 $\angle \mathit{BEO}=\angle \mathit{ABC}$ ，求点 $E$ 的坐标．