江苏省连云港市东海县中考第一次模拟考试数学试卷
在平面直角坐标系中,点P(1,-1)关于原点的对称点的坐标为
| A.(1,1) | B.(1,-1) | C.(-1,1) | D.(-1,-1) |
下列运算正确的是
| A.x2÷x3=x2 | B.(-2x)3=-6x3 | C.2x2-x=x | D.(x3)3=x9 |
在反比例函数 的图像的每一条曲线上,
的图像的每一条曲线上,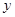 都随
都随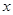 的增大而减小,则
的增大而减小,则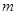 的值可以是
的值可以是
| A.0 | B.1 | C.2 | D.3 |
如图,点A、B、C都在⊙O上,⊙O的半径为2,∠ACB=30°,则弧AB的长是
A. B.
B. C.
C. D.
D.
下列事件是必然事件的是
A.若 ,则 ,则 |
| B.在常规情况下,将水加热到100℃时水会沸腾 |
| C.投掷一枚硬币,落地后正面朝上 |
| D.长为3cm、3cm、7cm的三条线段能围成一个三角形 |
将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是
| A.44° | B.45° | C.46° | D.54° |
小敏在“百度”搜索引擎中输入“水晶之都”,能搜索到与之相关的结果信息个数约为4 460 000,这个数用科学记数法表示为 .
一天,小青在校园内发现一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图所示).如果小青的身高为1.5米,由此可推断出树高是 米.
如图,由边长为1的小正方形组成的网格中, A、B、C三点都在网格的格点上.则tan∠BAC= .
用火柴棒摆成如图所示的三个“中”字形图案,依次规律,第n个“中”字形图案需要 .
根火柴棒(用含n的代数式表示).
(本题8分)某校学生会为了了解学生上网时间情况,从全校3600名学生中随机选取一部分学生进行调查.调查时将每周上网时间情况分为:A:上网时间≤1小时;B:1小时<上网时间≤4小时;C:4小时<上网时间≤7小时;D:上网时间>7小时.根据统计结果制成了如下统计图:
(1)参加调查的学生有 人;
(2)请将条形统计图补全;
(3)请估计全校每周上网不超过7小时的学生人数.
(本题8分)4张奖券中有2张是有奖的,甲、乙先后各抽一张.
(1)甲中奖的概率是 ;
(2)试用列树状图或列表法求甲、乙都中奖的概率.
(本题10分)如图,在⊙O中,AB为直径,AC为弦,过点C作CD⊥AB于点D,将△ACD沿AC翻折,点D落在点E处,AE交⊙O于点F ,连接OC、FC.
(1)求证:CE是⊙O的切线.
(2)若FC∥AB,求证:四边形 AOCF是菱形.
(本题10分)如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.
(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?
(参考数据:sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
(本题12分) 某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使
前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
(本题12分)如图1,直线y=﹣3x+6与x轴、y轴分别交于点A、B,抛物线 y=a(x﹣4)2+k
经过点A、B,并与x轴交于另一点C,其顶点为D.

(1)则a= ,k= ;(直接填空)
(2)抛物线的对称轴上是否存在一点P,使△ABP是以AB为斜边的直角三角形,若存在,求P点的坐
标;若不存在,说明理由.
(3)如图2,连接AD、DC、CB,经过点A存在一条直线将四边形ABCD的面积分为3:5的两个部分,
试求这条直线的函数关系式.
(本题14分)小明在学习平行线相关知识时总结了如下结论:端点分别在两条平行线上的所有线段中,垂直于平行线的线段最短.
小明应用这个结论进行了下列探索活动和问题解决.
问题1:如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AC边上的一动点,以PB,PA为边构造
□APBQ,求对角线PQ的最小值及PQ最小时 的值.
的值.
(1)在解决这个问题时,小明构造出了如图2的辅助线,则PQ的最小值为 ,当PQ最小时 = _____ __;
= _____ __;
(2)小明对问题1做了简单的变式思考.如图3,P为AB边上的一动点,延长PA到点E,使AE=nPA(n
为大于0的常数).以PE,PC为边作□PCQE,试求对角线PQ长的最小值,并求PQ最小时 的值;
的值;
问题2:在四边形ABCD中,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
(1)如图4,若 为
为 上任意一点,以
上任意一点,以 ,
, 为边作□
为边作□ .试求对角线
.试求对角线 长的最小值和PQ最小时
长的最小值和PQ最小时 的值.
的值.
(2)若 为
为 上任意一点,延长
上任意一点,延长 到
到 ,使
,使 ,再以
,再以 ,
, 为边作□
为边作□ .请直接写出对角线
.请直接写出对角线 长的最小值和PQ最小时
长的最小值和PQ最小时 的值.
的值.





 在实数范围内有意义,则x的取值范围是 .
在实数范围内有意义,则x的取值范围是 . 化为整式方程,方程两边可以同时乘以最简公分母 .
化为整式方程,方程两边可以同时乘以最简公分母 . 和反比例函数
和反比例函数 (
( ∙
∙ ≠0)的图像如图所示,若
≠0)的图像如图所示,若 >
> , 则
, 则 的取值范围是 .
的取值范围是 .
 .
. ,其中
,其中
 的解集,并将解集在数轴上表示.
的解集,并将解集在数轴上表示. 和△
和△ 中,
中, ,
, ,
, ,点
,点 在
在 上.
上.
 ≌△
≌△ ;
; .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号