(本题10分)如图,在⊙O中,AB为直径,AC为弦,过点C作CD⊥AB于点D,将△ACD沿AC翻折,点D落在点E处,AE交⊙O于点F ,连接OC、FC.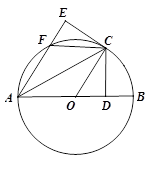
(1)求证:CE是⊙O的切线.
(2)若FC∥AB,求证:四边形 AOCF是菱形.
推荐套卷
(本题10分)如图,在⊙O中,AB为直径,AC为弦,过点C作CD⊥AB于点D,将△ACD沿AC翻折,点D落在点E处,AE交⊙O于点F ,连接OC、FC.
(1)求证:CE是⊙O的切线.
(2)若FC∥AB,求证:四边形 AOCF是菱形.