(本题14分)小明在学习平行线相关知识时总结了如下结论:端点分别在两条平行线上的所有线段中,垂直于平行线的线段最短.
小明应用这个结论进行了下列探索活动和问题解决.
问题1:如图1,在Rt△ABC中,∠C=90°,AC=4,BC=3,P为AC边上的一动点,以PB,PA为边构造
□APBQ,求对角线PQ的最小值及PQ最小时 的值.
的值.
(1)在解决这个问题时,小明构造出了如图2的辅助线,则PQ的最小值为 ,当PQ最小时 = _____ __;
= _____ __;
(2)小明对问题1做了简单的变式思考.如图3,P为AB边上的一动点,延长PA到点E,使AE=nPA(n
为大于0的常数).以PE,PC为边作□PCQE,试求对角线PQ长的最小值,并求PQ最小时 的值;
的值;
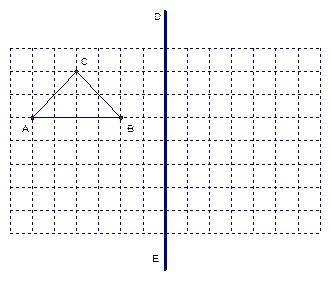
问题2:在四边形ABCD中,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.
(1)如图4,若 为
为 上任意一点,以
上任意一点,以 ,
, 为边作□
为边作□ .试求对角线
.试求对角线 长的最小值和PQ最小时
长的最小值和PQ最小时 的值.
的值.
(2)若 为
为 上任意一点,延长
上任意一点,延长 到
到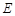 ,使
,使 ,再以
,再以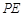 ,
, 为边作□
为边作□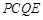 .请直接写出对角线
.请直接写出对角线 长的最小值和PQ最小时
长的最小值和PQ最小时 的值.
的值.
推荐套卷
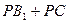 最小
最小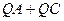 最小
最小





 粤公网安备 44130202000953号
粤公网安备 44130202000953号