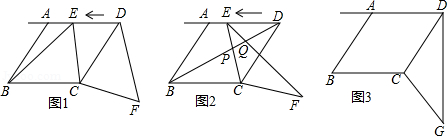
如图1,在菱形 中, , ,点 从点 出发,以每秒1个单位长度的速度沿着射线 的方向匀速运动,设运动时间为 (秒 ,将线段 绕点 顺时针旋转一个角 ,得到对应线段 .
(1)求证: ;
(2)当 秒时, 的长度有最小值,最小值等于 ;
(3)如图2,连接 、 、 交 、 于点 、 ,当 为何值时, 是直角三角形?
(4)如图3,将线段 绕点 顺时针旋转一个角 ,得到对应线段 .在点 的运动过程中,当它的对应点 位于直线 上方时,直接写出点 到直线 的距离 关于时间 的函数表达式.
相关知识点
推荐套卷

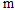 ),解答下列问题:
),解答下列问题:
 ,且地面总面积是卫生间面积的15倍,铺1
,且地面总面积是卫生间面积的15倍,铺1
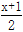 -1=
-1=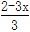 .
.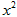 -[7x-2(6x-8)-
-[7x-2(6x-8)- 粤公网安备 44130202000953号
粤公网安备 44130202000953号