如图,在直角梯形OABC中,已知B、C两点的坐标分别为B(8,6)、C(10,0),动点M由原点O出发沿OB方向匀速运动,速度为1单位/秒;同时,线段DE由BC出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM,设运动时间为t秒(0<t<8). 
(1) 当 为何值时,DM∥OA?
为何值时,DM∥OA?
(2)连接ME,在点M、N重合之前的运动过程中,五边形DMECB的面积是否发生变化?若不变,请求出它的值;若发生变化,请说明理由.
(3)当t为何值时,△DMB为等腰三角形.
已知:直角梯形 中,
中,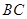 ∥
∥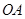 ,∠
,∠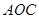 =
=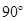 ,以
,以 为直径的圆
为直径的圆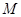 交
交 于点
于点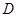 、
、 ,连结
,连结 、
、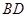 、
、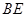 .
.
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形:
_____________________,______________________ ;
(2)直角梯形 中,以
中,以 为坐标原点,
为坐标原点,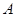 在
在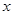 轴正半轴上建立直角坐标系(如图2),若抛物线
轴正半轴上建立直角坐标系(如图2),若抛物线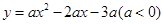 经过点
经过点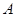 、
、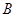 、
、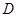 ,且
,且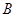 为抛物线的顶点.
为抛物线的顶点.
①写出顶点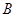 的坐标(用含
的坐标(用含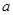 的代数式表示)___________;
的代数式表示)___________;
②求抛物线的解析式;
③在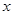 轴下方的抛物线上是否存在这样的点
轴下方的抛物线上是否存在这样的点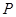 ,过点
,过点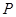 作
作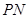 ⊥
⊥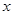 轴于点
轴于点 ,使得以点
,使得以点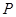 、
、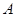 、
、 为顶点的三角形与△
为顶点的三角形与△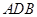 相似?
相似?
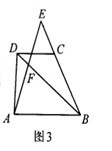
如图,在菱形ABCD中,∠C=60°,AB=4,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=60°. 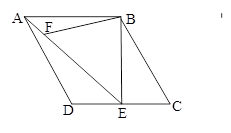
(1)求证:△ABF∽△EAD;
(2)求BF的长.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,连接OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.
(1)求证:OD∥AC;
(2)当AB=10,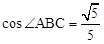 时,求AF及BE的长.
时,求AF及BE的长.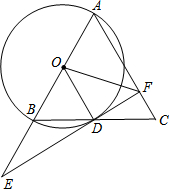
如图,已知 中,
中, ,
, ,
, ,
, 是
是 边上的中点,
边上的中点, 是
是 边上的点(不与端点重合),
边上的点(不与端点重合), 是
是 边上的点,且
边上的点,且 ∥
∥ ,延长
,延长 与直线
与直线 相交于点
相交于点 ,
, 点是
点是 延长线上的点,且
延长线上的点,且 ,联结
,联结 ,设
,设 ,
, .
.
(1)求 关于
关于 的函数关系式及其定义域;
的函数关系式及其定义域;
(2)联结 ,当以
,当以 为半径的
为半径的 和以
和以 为半径的
为半径的 外切时,求
外切时,求 的正切值;
的正切值;
(3)当 与
与 相似时,求
相似时,求 的长.
的长.
(年新疆乌鲁木齐14分)如图.在平面直角坐标系中,边长为 的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
的正方形ABCD的顶点A、B在x轴上,连接OD、BD、△BOD的外心I在中线BF上,BF与AD交于点E.
(1)求证:△OAD≌△EAB;
(2)求过点O、E、B的抛物线所表示的二次函数解析式;
(3)在(2)中的抛物线上是否存在点P,其关于直线BF的对称点在x轴上?若有,求出点P的坐标;
(4)连接OE,若点M是直线BF上的一动点,且△BMD与△OED相似,求点M的坐标.
如图, AE是⊙O直径,D是⊙O上一点,连结AD并延长使AD=DC,连结CE交⊙O于点B,连结AB.过点E的直线与AC的延长线交于点F,且∠F=∠CED.
(1)求证:EF是⊙O切线;
(2)若CD=CF=2,求BE的长.
如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,边AE上有一动点P(不与A,E重合)自A点沿AE方向向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE的平行线交DE于点N.

(1)直接写出 D,E 两点的坐标,D( ),E( )
(2)求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,S有最大值?
(3)当t为何值时,DP平分∠EDA?
(4)当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标.
如图,已知在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=11,BC=13,AB=12.动点P、Q分别在边AD和BC上,且BQ=2DP.线段PQ与BD相交于点E,过点E作EF∥BC,交CD于点F,射线PF交BC的延长线于点G,设DP=x.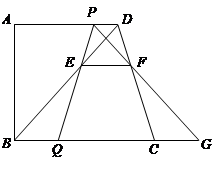
(1)求 的值.
的值.
(2)当点P运动时,试探究四边形EFGQ的面积是否会发生变化?如果发生变化,请用x的代数式表示四边形EFGQ的面积S;如果不发生变化,请求出这个四边形的面积S.
(3)当△PQG是以线段PQ为腰的等腰三角形时,求x的值.
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在□ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值.
的值.
(1)尝试探究
在图1中,过点E作 交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,
交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 , 的值是
的值是
(2)类比延伸
如图2,在原题的条件下,若 (m>0),则
(m>0),则 的值是 (用含
的值是 (用含 的代数式表示),试写出解答过程.
的代数式表示),试写出解答过程.
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若 ,
, (
( ,
, ),则
),则 的值是 (用含a、b的代数式表示).
的值是 (用含a、b的代数式表示).


已知,如图,以点P(﹣1,0)为圆心的圆,交x轴于A、C两点(A在C的左侧),交y轴于B、D两点(B在D的上方),且∠BAC=30°,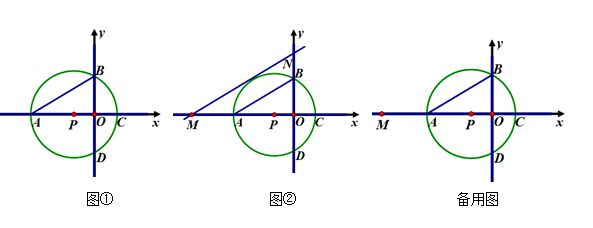
(1)如图①求⊙P的半径及点B的坐标;
(2)点Q是⊙P上任意一点,求△ABQ面积S的取值范围;
(3)如图②,已知点M(-5,0),过M作直线y=kx+b交y轴于点N,
①若MN//AB,试判断MN与⊙P的位置关系,并说明理由;
②在该直线上存在一点G,使以G、A、C为顶点的三角形是直角三角形,且满足条件的点G有且只有三个不同位置,求直线MN的函数关系式.
(本题14分)如图,在等边 中,
中, 于点
于点 ,点
,点 在边
在边 上运动,过点
上运动,过点 作
作 与边
与边 交于点
交于点 ,连结
,连结 ,以
,以 为邻边作□
为邻边作□ ,设□
,设□ 与
与 重叠部分图形的面积为
重叠部分图形的面积为 ,线段
,线段 的长为
的长为

(1)求线段 的长(用含
的长(用含 的代数式表示);
的代数式表示);
(2)当四边形 为菱形时,求
为菱形时,求 的值;
的值;
(3)直接写出 与
与 之间的函数关系式.
之间的函数关系式.
如图,直线l经过点A(1,0),且与双曲线y= (x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交曲线y=
(x>0)交于点B(2,1),过点P(p,p-1)(p>1)作x轴的平行线分别交曲线y= (x>0)和y=-
(x>0)和y=- (x<0)于M,N两点.
(x<0)于M,N两点.

(1)求m的值及直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA;
(3)是否存在实数p,使得S△AMN=4S△APM?若存在,请求出所有满足条件的p的值;若不存在,请说明理由.
如图,已知左右并排的两棵树高分别是AB=8m,CD=12m,两树的根部的距离BD=5m,小明眼睛离地面的高度EF为1.6m,他沿着正对这两棵树的一条水平直路从左到右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C? 
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是斜边AB上的一个动点(点P与点A、B不重合),以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,射线PD交射线BC于点E.
(1)如图1,若点E在线段BC的延长线上,设AP=x,CE=y,
①求y关于x的函数关系式,并写出x的取值范围;
②当以BE为直径的圆和⊙P外切时,求AP的长;
(2)设线段BE的中点为Q,射线PQ与⊙P相交于点I,若CI=AP,求AP的长.