如图,在直角梯形OABC中,已知B、C两点的坐标分别为B(8,6)、C(10,0),动点M由原点O出发沿OB方向匀速运动,速度为1单位/秒;同时,线段DE由BC出发沿BA方向匀速运动,速度为1单位/秒,交OB于点N,连接DM,设运动时间为t秒(0<t<8). 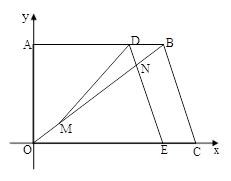
(1) 当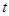 为何值时,DM∥OA?
为何值时,DM∥OA?
(2)连接ME,在点M、N重合之前的运动过程中,五边形DMECB的面积是否发生变化?若不变,请求出它的值;若发生变化,请说明理由.
(3)当t为何值时,△DMB为等腰三角形.
相关知识点
推荐套卷

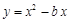 与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.
与x轴正半轴相交于点A,点B(m,-3)为抛物线上一点,△OAB的面积等于6.

 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号