如图,在△ABC中,AC = BC,AB = 8,CD⊥AB,垂足为点D.M为边AB上任意一点,点N在射线CB上(点N与点C不重合),且MC = MN.设AM = x.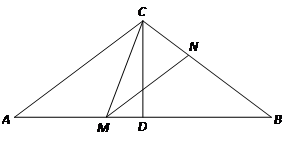
(1)如果CD = 3,AM = CM,求AM的长;
(2)如果CD = 3,点N在边BC上.设CN = y,求y与x的函数解析式,并写出函数的定义域;
(3)如果∠ACB = 90°,NE⊥AB,垂足为点E.当点M在边AB上移动时,试判断线段ME的长是否会改变?说明你的理由.
相关知识点
推荐套卷
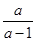 ÷
÷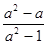 -
-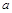 =-
=-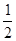 .
. ,把它的解集在数轴上表示出来,并求其整数解.
,把它的解集在数轴上表示出来,并求其整数解.
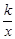 的图象交于点A(3,2).
的图象交于点A(3,2).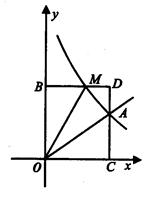
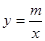 的图象的交点.
的图象的交点.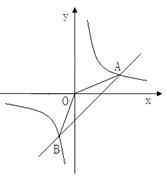
 粤公网安备 44130202000953号
粤公网安备 44130202000953号